
| A. | 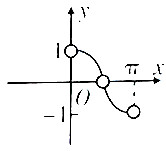 | B. | 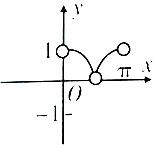 | ||
| C. | 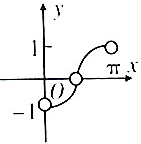 | D. | 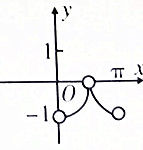 |
分析 根据函数的定义域,在区间(0,$\frac{π}{2}$)上,y=cosx∈(0,1),且函数y单调递减;在区间($\frac{π}{2}$,π)上,y=-cosx∈(0,1),且函数y单调递增,结合所给的选项,得出结论.
解答 解:由于函数y=$\frac{sinx}{|tanx|}$ (0<x<π,x≠$\frac{π}{2}$),∴tanx≠0,且sinx≠0,
∴函数的定义域为{x|x≠kπ,且x≠kπ+$\frac{π}{2}$,k∈Z}.
在区间(0,$\frac{π}{2}$)上,y=cosx∈(0,1),且函数y单调递减;
在区间($\frac{π}{2}$,π)上,y=-cosx∈(0,1),且函数y单调递增,
结合所给的选项,
故选:B.
点评 本题主要考查带有绝对值的函数,函数的定义域和值域,函数的单调性,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
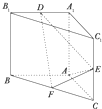 如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1,CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1,CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的分数三角形,称为“莱布尼茨三角形”.这个三角形的规律是:各行中的每一个数,都等于后面一行中与它相邻的两个数之和(例如第4行第2个数$\frac{1}{12}$等于第5行中的第2个数$\frac{1}{20}$与第3个数$\frac{1}{30}$之和).则
如图所示的分数三角形,称为“莱布尼茨三角形”.这个三角形的规律是:各行中的每一个数,都等于后面一行中与它相邻的两个数之和(例如第4行第2个数$\frac{1}{12}$等于第5行中的第2个数$\frac{1}{20}$与第3个数$\frac{1}{30}$之和).则| A. | 5010 | B. | 5020 | C. | 10120 | D. | 10130 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com