
【题目】已知函数![]() .
.
(1)判断![]() 的图象是否是中心对称图形?若是,求出对称中心;若不是,请说明理由;
的图象是否是中心对称图形?若是,求出对称中心;若不是,请说明理由;
(2)设![]() ,试讨论
,试讨论![]() 的零点个数情况.
的零点个数情况.
【答案】(1)![]() 的图象是中心对称图形,对称中心为:
的图象是中心对称图形,对称中心为:![]() ;(2)当
;(2)当![]() 或
或![]() 时,有
时,有![]() 个零点;当
个零点;当![]() 时,有
时,有![]() 个零点
个零点
【解析】
(1)设![]() ,通过奇偶性的定义可求得
,通过奇偶性的定义可求得![]() 为奇函数,关于原点对称,从而可得
为奇函数,关于原点对称,从而可得![]() 的对称中心,得到结论;(2)
的对称中心,得到结论;(2)![]() ,可知
,可知![]() 为一个解,从而将问题转化为
为一个解,从而将问题转化为![]() 解的个数的讨论,即
解的个数的讨论,即![]() 的解的个数;根据
的解的个数;根据![]() 的范围,分别讨论不同范围情况下方程解的个数,从而得到零点个数,综合得到结果.
的范围,分别讨论不同范围情况下方程解的个数,从而得到零点个数,综合得到结果.
(1) 设![]()
![]() 定义域为:
定义域为:![]()
![]()
![]() 为奇函数,图象关于
为奇函数,图象关于![]() 对称
对称
![]() 的图象是中心对称图形,对称中心为:
的图象是中心对称图形,对称中心为:![]()
(2)令![]()
 ,可知
,可知![]() 为其中一个解,即
为其中一个解,即![]() 为一个零点
为一个零点
只需讨论![]() 的解的个数即可
的解的个数即可
①当![]() 时,
时,![]() 无解
无解
![]() 有且仅有
有且仅有![]() 一个零点
一个零点
②当![]() 时 ,
时 ,![]()
![]() 为方程
为方程![]() 的解
的解
![]() 有
有![]() ,
,![]() 共
共![]() 个零点
个零点
③当![]() 时,
时,![]()
(i)若![]() ,即
,即![]() 时,
时,![]()
![]() 为方程
为方程![]() 的解
的解
![]() 有
有![]() ,
,![]() 共
共![]() 个零点
个零点
(ii)若![]() ,即
,即![]() 时,
时,![]() 的解为:
的解为:![]()
![]() 有且仅有
有且仅有![]() 一个零点
一个零点
(iii)若![]() ,即
,即![]() 时,
时,![]() ,方程
,方程![]() 无解
无解
![]() 有且仅有
有且仅有![]() 一个零点
一个零点
综上所述:当![]() 或
或![]() 时,有
时,有![]() 个零点;当
个零点;当![]() 时,有
时,有![]() 个零点
个零点


科目:高中数学 来源: 题型:
【题目】每年的3月21日被定为“世界睡眠日”,拥有良好睡眠对人的健康至关重要,一夜好眠成为很多现代人的诉求.某市健康研究机构于2018年3月14日到3月20日持续一周,通过网络调查该市20岁至60岁市民的日平均睡眠时间![]() (单位:小时),共有500人参加调查,其中年龄在区间
(单位:小时),共有500人参加调查,其中年龄在区间![]() 的有200人,现将调查数据统计整理后,得到如下频数分布表:
的有200人,现将调查数据统计整理后,得到如下频数分布表:

(1)根据上表,在给定坐标系中画出这500名市民日平均睡眠时间的频率分布直方图;
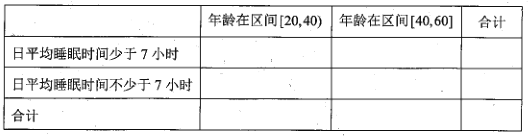
(2)填写下面![]() 列联表,并根据
列联表,并根据![]() 列联表判断是否有99%的把握认为该市20岁至60岁市民的日平均睡眠时间与年龄有关;
列联表判断是否有99%的把握认为该市20岁至60岁市民的日平均睡眠时间与年龄有关;

![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0,则称x0是f(x)的一个不动点,已知f(x)=x2+ax+4在[1,3]恒有两个不同的不动点,则实数a的取值范围______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在坐标原点,焦点 ![]() ,
,![]() 在坐标轴上,离心率为
在坐标轴上,离心率为![]() ,且过点
,且过点![]() .
.
(1) 求双曲线的标准方程;
(2) 若点![]() 在第一象限且是渐近线上的点,当
在第一象限且是渐近线上的点,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=x-(a+1)ln x-![]() (a∈R),g (x)=
(a∈R),g (x)=![]() x2+ex-xex.
x2+ex-xex.
(1)当x∈[1,e] 时,求f (x)的最小值;
(2)当a<1时,若存在x1∈[e,e2],使得对任意的x2∈[-2,0],f (x1)<g (x2)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列的定义可用数学符号语言描述为_______,其中![]() ,其通项公式
,其通项公式![]() _________,
_________,![]() ______,等比数列中,若
______,等比数列中,若![]() 则_________(
则_________(![]() ),若
),若![]() ,则
,则![]() 的等比中项为____.
的等比中项为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1-20这20个整数中随机选择一个数,设事件A表示选到的数能被2整除,事件B表示选到的数能被3整除,求下列事件的概率;
(1)这个数既能被2整除也能被3整除;
(2)这个数能被2整除或能被3整除;
(3)这个数既不能被2整除也不能被3整除.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com