Question

【题目】已知四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD=60°，AB=PB=PD=2， ．
（Ⅰ）求证：BD⊥PC；
（Ⅱ）若E是PA的中点，求二面角A﹣EC﹣B的余弦值．

Answer 1

【答案】（Ⅰ）证明：设AC，BD交点为O，连接PO，
∵四边形ABCD是菱形，∴AC⊥BD，O是AC、BD的中点，
∵PB=PD，∴PO⊥BD，
又PO平面POC，AC平面POC，PO∩AC=O，
∴BD⊥平面POC，∵PC平面POC，
∴BD⊥PC．
（Ⅱ）解：∠BAD=60°，AB=AD=2，
∴△ABD是等边三角形，
又AB=PB=PD，
∴△PBD是等边三角形，
∴OA=OP= ，
∴OA2+OP2=PA2 ， ∴OA⊥OP，
又OP⊥OB，OA∩OB=O，
∴OP⊥平面ABCD．
以O为原点，以OB，OC，OP为坐标轴建立空间直角坐标系如图：
则A（0，﹣ ，0），B（1，0，0），C（0， ，0），P（0，0， ），
∵E是PA的中点，∴E（0，﹣ ， ），
∴ =（0，﹣ ， ）， =（﹣1， ，0），
设平面BCE的法向量为 =（x，y，z），则 ，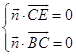
∴ ，令y=1得 =（ ，1，3），
又BD⊥平面POC，
∴ =（1，0，0）是平面ACE的一个法向量，
∴cos＜ ＞= = = ，
∵二面角A﹣EC﹣B为锐二面角，
∴二面角A﹣EC﹣B的余弦值为
【解析】（Ⅰ）由BD⊥AC，BD⊥PO即可得出BD⊥平面PAC，故而BD⊥PC；（Ⅱ）证明OP⊥平面ABCD，建立空间坐标系，求出两平面的法向量的夹角，从而得出二面角的大小．
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本，需要知道相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．