
【题目】设椭圆![]() :
:![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 为短轴端点,且
为短轴端点,且![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程,
的方程,
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点![]() ,
,![]() ,且满足
,且满足![]() ?若存在,求出该圆的方程,若不存在,说明理由.
?若存在,求出该圆的方程,若不存在,说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由题意可得方程![]() 2cb=4,e
2cb=4,e![]() ,且a2=b2+c2;从而联立解出椭圆C的方程为
,且a2=b2+c2;从而联立解出椭圆C的方程为![]() 1;
1;
(2)假设存在圆心在原点的圆x2+y2=r2,使得该圆的任意一条切线与椭圆C恒有两个交点M、N,则可得![]()
![]() 0;再设M(x1,y1),N(x2,y2),当切线斜率存在时,设该圆的切线的方程为y=kx+m,与椭圆联立,利用韦达定理及条件可得3m2﹣8k2﹣8=0,代入△从而可解得m的范围,进而解出所求圆的方程,再验证当切线的斜率不存在时也成立即可.
0;再设M(x1,y1),N(x2,y2),当切线斜率存在时,设该圆的切线的方程为y=kx+m,与椭圆联立,利用韦达定理及条件可得3m2﹣8k2﹣8=0,代入△从而可解得m的范围,进而解出所求圆的方程,再验证当切线的斜率不存在时也成立即可.
(1))∵椭圆C:![]() 1(a>b>0),
1(a>b>0),
由题意可得,
![]() 2cb=4,e
2cb=4,e![]() ,且a2=b2+c2;
,且a2=b2+c2;
联立解得,![]() ;
;
故椭圆C的方程为![]() 1;
1;
(2)假设存在圆心在原点的圆x2+y2=r2,
使得该圆的任意一条切线与椭圆C恒有两个交点M、N,
∵|![]() |=|
|=|![]() |,
|,
∴![]()
![]() 0;
0;
设M(x1,y1),N(x2,y2),
当切线斜率存在时,设该圆的切线的方程为y=kx+m,
解方程组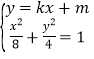 得,
得,
(1+2k2)x2+4kmx+2m2﹣8=0,
则△=(4km)2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0;
即8k2﹣m2+4>0;
∴x1+x2![]() ,x1x2
,x1x2![]() ;
;
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2![]() ;
;
要使![]()
![]() 0,
0,
故x1x2+y1y2=0;
即![]() 0;
0;
所以3m2﹣8k2﹣8=0,
所以3m2﹣8≥0且8k2﹣m2+4>0;
解得m![]() 或m
或m![]() ;
;
因为直线y=kx+m为圆心在原点的圆的一条切线,
所以圆的半径为r![]() ,r2
,r2![]() ;
;
故r![]() ;
;
即所求圆的方程为x2+y2![]() ;
;
此时圆的切线y=kx+m都满足m![]() 或m
或m![]() ;
;
而当切线的斜率不存在时切线为x=±![]() 与椭圆
与椭圆![]() 1的两个交点为(
1的两个交点为(![]() ,±
,±![]() ),(
),(![]() ,±
,±![]() );
);
满足![]()
![]() 0,
0,
综上所述,存在圆心在原点的圆x2+y2![]() 满足条件.
满足条件.


科目:高中数学 来源: 题型:
【题目】下列结论中不正确的是( )
A.若两个平面有一个公共点,则它们有无数个公共点
B.若已知四个点不共面,则其中任意三点不共线
C.若点![]() 既在平面
既在平面![]() 内,又在平面
内,又在平面![]() 内,则
内,则![]() 与
与![]() 相交于
相交于![]() ,且点
,且点![]() 在
在![]() 上
上
D.任意两条直线不能确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为![]() 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.

(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像如图所示,关于
的图像如图所示,关于![]() 有以下5个结论:
有以下5个结论:

(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)将图像上所有点向右平移
;(3)将图像上所有点向右平移![]() 个单位得到的图形所对应的函数是偶函数;(4)对于任意实数x都有
个单位得到的图形所对应的函数是偶函数;(4)对于任意实数x都有![]() ;(5)对于任意实数x都有
;(5)对于任意实数x都有![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )
A.(1)(2)(3)B.(1)(2)(4)(5)C.(1)(2)(4)D.(1)(3)(4)(5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
运动达人 | 参与者 | 合计 | |
男教师 | 60 | 20 | 80 |
女教师 | 40 | 20 | 60 |
合计 | 100 | 40 | 140 |
(Ⅰ)根据上表说明,能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关?
(Ⅱ)从具有“运动达人”称号的教师中,采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动,若从选取的10人中随机抽取3人作为代表参加开幕式,设抽取的3人中女教师人数为![]() ,写出
,写出![]() 的分布列并求出数学期望
的分布列并求出数学期望![]() .
.
参考公式: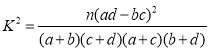 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线C1的参数方程为![]() (t为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆C2的方程为ρ=﹣2cosθ+2
(t为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆C2的方程为ρ=﹣2cosθ+2![]() sinθ.
sinθ.
(Ⅰ)求直线C1的普通方程和圆C2的圆心的极坐标;
(Ⅱ)设直线C1和圆C2的交点为A,B,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张矩形白纸ABCD,AB=10,AD=![]() ,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)
,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)

①当平面ABE∥平面CDF时,AC∥平面BFDE
②当平面ABE∥平面CDF时,AE∥CD
③当A、C重合于点P时,PG⊥PD
④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com