
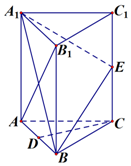
 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.分析 (1)设AB1和A1B的交点为O,连接EO,连接OD,易得四边形ECDO为平行四边形,即EO∥CD.得到OD∥平面A1BE.
(2)证明EO⊥AB1. AB1⊥A1B.即可得到AB1⊥平面A1BE
解答  解:(1)设AB1和A1B的交点为O,连接EO,连接OD,因为O为AB1的中点,D为AB的中点,所以OD∥BB1,且$OD=\frac{1}{2}B{B_1}$又E是CC1中点,则EC∥BB1
解:(1)设AB1和A1B的交点为O,连接EO,连接OD,因为O为AB1的中点,D为AB的中点,所以OD∥BB1,且$OD=\frac{1}{2}B{B_1}$又E是CC1中点,则EC∥BB1
且$EC=\frac{1}{2}B{B_1}$,所以EC∥OD且EC=OD.所以四边形ECDO为平行四边形,
所以EO∥CD. …(4分)
又CD?平面A1BE,EO?平面A1BE,则CD∥平面A1BE…(7分)
(2)因为正三棱柱,所以BB1⊥平面ABC.因为CD?平面ABC,
所以BB1⊥CD.由已知得AB=BC=AC,所以CD⊥AB.
所以CD⊥平面A1ABB1由(1)可知EO∥CD,所以EO⊥平面A1ABB1所以EO⊥AB1. …(11分)
因为正三棱柱各棱长相等,所以侧面是正方形,所以AB1⊥A1B.
又EO∩A1B=O,EO?平面A1EB,A1B?平面A1EB.所以AB1⊥平面A1BE. …(14分)
点评 本题考查了空间线面平行、线面垂直的判定,转化思想是解题的关键,属于中档题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值 $\frac{{11+2\sqrt{10}}}{3}$ | B. | 有最大值$\frac{{11+2\sqrt{10}}}{3}$ | ||
| C. | 有最小值$\frac{{11-2\sqrt{10}}}{3}$ | D. | 有最大值$\frac{{11-2\sqrt{10}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com