
【题目】如图,正方体 ![]() 中,
中, ![]() 分别为
分别为 ![]() 的中点.
的中点.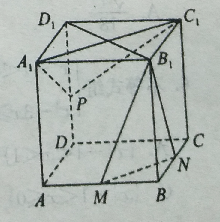
(1)求证:平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(2)当点 ![]() 在
在 ![]() 上运动时,是否都有
上运动时,是否都有 ![]() 平面
平面 ![]() ,证明你的结论;
,证明你的结论;
(3)若 ![]() 是
是 ![]() 的中点,试判断
的中点,试判断 ![]() 与平面
与平面 ![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
【答案】
(1)证明:正方体 ![]() 中,
中, ![]() 平面
平面 ![]() ,
,
![]() 平面
平面 ![]() ,所以
,所以 ![]() ,
,
连接 ![]() ,因为
,因为 ![]() 分别为
分别为 ![]() 的中点,
的中点,
所以 ![]() ,
,
又四边形 ![]() 是正方形,所以
是正方形,所以 ![]() ,所以
,所以 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() 平面
平面 ![]() ,
,
又因为 ![]() 平面
平面 ![]() ,所以平面
,所以平面 ![]() 平面
平面 ![]() ,
,
(2)解:当点 ![]() 在
在 ![]() 上移动时,都有
上移动时,都有 ![]() 平面
平面 ![]() ,证明如下:
,证明如下:
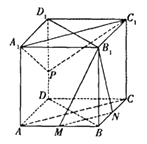
在正方体中 ![]() ,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
,A1A∥C1C,且A1A=C1C,所以A1ACC1为平行四边形,
所以A1 C1∥A C,
由(1)知,MN∥A C,所以MN∥A1 C1
又 ![]()
所以 ![]()
(3)解:PB⊥平面B1MN
设 ![]() 的中点为Q,连接PQ,则PQ⊥平面
的中点为Q,连接PQ,则PQ⊥平面 ![]() B1B
B1B
再连接BQ,因为Q,M分别为 ![]() ,AB的中点
,AB的中点
所以△BB1M≌△ABQ
所以∠BB1M=∠ABQ,所以∠ABQ+∠BMB1=90°
所以B1M⊥BQ,又PQ⊥平面 ![]() B1B,所以PQ⊥B1M
B1B,所以PQ⊥B1M
所以B1M⊥平面PBQ
所以B1M⊥PB,又由(1)知, MN⊥平面BB1D1D,所以MN⊥PB
所以PB⊥平面B1MN
【解析】(1)根据题意作出辅助线结合已知可得 M N / / A C即 M N ⊥ B D ,利用线面垂直的判定定理可得出M N ⊥ 平面 B B1 D1 D,进而由面面垂直的判定定理即可得证。(2)当当点 P 在 D1 D 上运动时,都有 M N / / 平面 A1 C 1P.利用线面平行的判定定理即可证明。(3)要证明PB⊥平面B1MN需利用题设条件推导出B1M⊥BQ,PQ⊥B1M,由此能够证明PB⊥平面B1MN成立。
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形, ∠CDA=∠BAD=90°, ![]() ,M,N分别是PD,PB的中点.
,M,N分别是PD,PB的中点.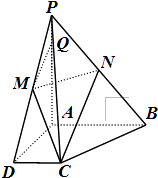
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: ①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 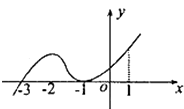
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在数列 ![]() 中,若
中,若 ![]()
![]() 为常数)则称
为常数)则称 ![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若 ![]() 是“等方差数列”,在数列
是“等方差数列”,在数列 ![]() 是等差数列;
是等差数列;
② ![]() 是“等方差数列”;
是“等方差数列”;
③若 ![]() 是“等方差数列”,则数列
是“等方差数列”,则数列 ![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若 ![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的(产品净重,单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,下列命题中:①样本中净重大于或等于98克并且小于102克的产品的个数是60;②样本的众数是101;③样本的中位数是 ![]() ; ④样本的平均数是101.3.
; ④样本的平均数是101.3.
正确命题的代号是(写出所有正确命题的代号).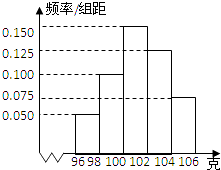
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 过点(1,e).
过点(1,e).
(1)求y=f(x)的单调区间;
(2)当x>0时,求 ![]() 的最小值;
的最小值;
(3)试判断方程f(x)﹣mx=0(m∈R且m为常数)的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x﹣4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于
=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x﹣4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于 ![]() ,则椭圆E的离心率的取值范围是( )
,则椭圆E的离心率的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[ ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com