设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列.
(Ⅰ)求数列{an}的公比q;
(Ⅱ)求证:a3,a9,a6成等差数列;
(Ⅲ)当am,as,at(m,s,t∈[1,10],m,s,t互不相等)成等差数列时,求m+s+t的值.
分析:(Ⅰ)由题意设出等比数列的前n项和公式,由S3,S9,S6成等差数列建立方程求q即可;
(Ⅱ)由(Ⅰ)给出a3,a9,a6的表达式,验证是否构成等差数列即可;
(Ⅲ)am,as,at(m,s,t∈[1,10],m,s,t互不相等)成等差数列时,由等差数列的性质构建方程,讨论既得.
解答:解:(Ⅰ)当q=1时,S
3=3a
1,S
9=9a
1,S
6=6a
1,
∵2S
9≠S
3+S
6,∴S
3,S
9,S
6不成等差数列,与已知矛盾,
∴q≠1.(2分)
由2S
9=S
3+S
6得:
2•=+,(4分)
即2(1-q
9)=(1-q
3)+(1-q
6)?2q
6-q
3-1=0,
∴
q3=-?q=-,q
3=1?q=1(舍去),∴
q=-(6分)
(Ⅱ)∵2a
9-a
3-a
6=2a
1q
8-a
1q
2-a
1q
5=a
1q
2(2q
6-1-q
3)=0,
∴2a
9=a
3+a
6,∴a
3,a
9,a
6成等差数列.(9分)
(Ⅲ)S
3,S
9,S
6成等差数列?2q
6-q
3-1=0?2q
6=q
3+1?2a
1q
6=a
1q
3+a
1?2a
7=a
4+a
1,
∴a
1,a
7,a
4成等差数列或a
4,a
7,a
1成等差数列,则m+s+t=12,(11分)
同理:a
2,a
8,a
5成等差数列或a
5,a
8,a
2成等差数列,则m+s+t=15,
a
3,a
9,a
6成等差数列或a
6,a
9,a
3成等差数列,则m+s+t=18,
a
4,a
10,a
7成等差数列或a
7,a
10,a
4成等差数列,则m+s+t=21,
∴m+s+t的值为12,15,18,21.(15分)
点评:本题考查等差与等比数列的综合运用,用到了分类讨论的思想,综合性较强.本题解题时容易因为讨论不全出错.



 名校课堂系列答案
名校课堂系列答案 ,则
,则 等于( )
等于( )



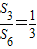 ,则
,则 等于( )
等于( )


