
【题目】如图,已知抛物线![]() ,设直线
,设直线![]() 经过点
经过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 、
、![]() 两点处的切线相交于点
两点处的切线相交于点![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

(1)求点![]() 的轨迹方程
的轨迹方程
(2)当点![]() 不在
不在![]() 轴上时,记
轴上时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)4
(2)4
【解析】
(1)首先设出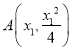 ,
, ,利用导数的几何意义求出切线
,利用导数的几何意义求出切线![]() ,
,![]() 的方程,联立得到交点
的方程,联立得到交点![]() 的坐标.再设出直线
的坐标.再设出直线![]() 的方程为
的方程为![]() ,代入抛物线,利用根系关系即可得到点
,代入抛物线,利用根系关系即可得到点![]() 的轨迹方程.
的轨迹方程.
(2)首先根据切线![]() ,
,![]() 的方程得到
的方程得到![]() ,
,![]() ,从而得到
,从而得到![]() ,
,![]() .利用弦长公式和点到直线的距离公式得到
.利用弦长公式和点到直线的距离公式得到![]() ,从而得到
,从而得到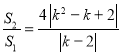 .令
.令![]() ,得到
,得到![]() ,再利用基本不等式即可得到
,再利用基本不等式即可得到![]() 的最值.
的最值.
(1)因为抛物线![]() ,所以
,所以![]() ,
,![]() .
.
设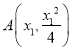 ,
, ,
,![]() ,
,![]() .
.
则切线![]() ,
,![]() 的方程分别为
的方程分别为![]() 和
和![]() .
.
联立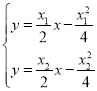 解得交点
解得交点![]() 的坐标为:
的坐标为:![]() ,
,![]() .
.
设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
整理得:![]() ,
,
所以![]() ,
,![]() ,且
,且![]() .
.
所以![]() ,
,![]() ,于是
,于是![]() ,
,
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)因为切线![]() 的方程为
的方程为![]() ,
,
令![]() 得到
得到![]() ,同理:
,同理:![]() .
.
所以![]() .
.
又![]() ,故
,故![]() .
.
由(1)可知![]() ,
,
又点![]() 到直线
到直线![]() 的距离为
的距离为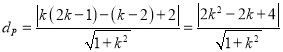 ,
,
所以![]() .
.
所以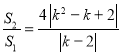 .
.
令![]() ,
,![]() ,则
,则 .
.
①当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”.
”.
所以![]() ;
;
②当![]() 时,
时,
![]() ,
,![]() ,
,![]() ,
,
当且仅当![]() 时取“
时取“![]() ”.
”.
所以![]() ;
;
综上所述:![]() 的最小值为
的最小值为![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 在
在![]() 处的切线的一般式方程;
处的切线的一般式方程;
(2)请判断![]() 与
与![]() 的图像有几个交点?
的图像有几个交点?
(3)设![]() 为函数
为函数![]() 的极值点,
的极值点,![]() 为
为![]() 与
与![]() 的图像一个交点的横坐标,且
的图像一个交点的横坐标,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极稳妥疫情期间的复学工作,市教育局抽调5名机关工作人员去某街道3所不同的学校开展驻点服务,每个学校至少去1人,若甲、乙两人不能去同一所学校,则不同的分配方法种数为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人玩掷正方体骰子走跳棋的游戏,已知骰子每面朝上的概率都是![]() ,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第
,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀骰子3次后,求棋子所走站数之和X的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第99站,则记选手落败,若最终棋子落在第100站,则记选手获胜,请分析这个游戏是否公平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为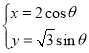 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求曲线![]() 上的动点到直线
上的动点到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 是过抛物线
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
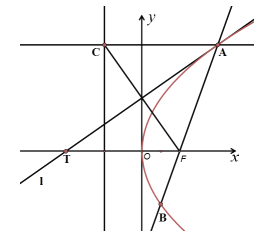
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com