【题目】已知在棱长为
的正方体
中，
分别是棱
，
的中点.
求证：（1）四边形
是梯形；
（2）
.
【答案】见解析．
【解析】
试题（1）结合三角形的中位线的性质得到MN=
AC，以及MN∥A1C1得到证明．
（2）由（1）可知MN∥A1C1，又∵ND∥A1D1，根据等角定理得到结论．
证明：（1）连接AC，在△ACD中，
∵M，N分别是棱CD，AD的中点，
∴MN是三角形的中位线，
∴MN∥AC，MN=AC．由正方体的性质得：AC∥A1C1，AC=A1C1．
∴MN∥A1C1，且MN=A1C1，即MN≠A1C1，∴四边形MN A1C1是梯形．
（2）由（1）可知MN∥A1C1，又∵ND∥A1D1，
∴∠DNM与∠D1A1C1相等或互补，而∠DNM与∠D1A1C1均是直角三角形的锐角，
∴∠DNM=∠D1A1C1
科目：高中数学 来源： 题型：
【题目】在△ABC中，BC边上的高所在直线的方程为x－2y＋1＝0，∠A的平分线所在的直线方程为y＝0．若点B的坐标为(1,2)，求点A和点C的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：x∈（-2，1），使等式x2-x-m=0成立，命题q：
表示椭圆．
（1）若命题p为真命题，求实数m的取值范围．
（2）判断命题p为真命题是命题q为真命题的什么条件（请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：y2=2x的焦点为F，过焦点F的直线交抛物线于A，B两点，过A，B作准线的垂线交准线与P，Q两点．R是PQ的中点．
（1）证明：以PQ为直径的圆恒过定点F．
（2）证明：AR∥FQ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数
的图像与x轴有两个不同的交点，其中一个交点坐标是
，且当
时，恒有
.
（1）求不等式
的解（用a、c表示）；
（2）若不等式
对所有
恒成立，求实数m的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，以坐标原点
为圆心的圆与直线：
相切.
（1）求圆的方程；
（2）若圆上有两点
关于直线
对称，且
,求直线MN的方程；
（3）圆与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】经市场调查，某商品在过去的100天内的销售量(单位：件)和价格(单位：元)均为时间
(单位：天)的函数，且销售量满足
=
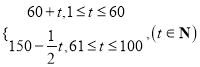，价格满足
=
．
(1)求该种商品的日销售额
与时间的函数关系；
(2)若销售额超过16610元，商家认为该商品的收益达到理想程度，请判断该商品在哪几天的收益达到理想程度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
