
【题目】已知函数![]() .
.
(1)若![]() ,试判断
,试判断![]() 的符号;
的符号;
(2)讨论![]() 的零点的个数.
的零点的个数.
【答案】(1)答案不唯一,具体见解析(2)当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点;当
个零点;当![]() 且
且![]() 时,
时,![]() 有
有![]() 个零点
个零点
【解析】
(1)首先计算得到![]() ,设
,设![]() ,利用二次求导,判断函数的单调性,
,利用二次求导,判断函数的单调性,![]() 和
和![]() 比较大小;
比较大小;
(2)首先求函数的导数![]() ,讨论
,讨论![]() ,
,![]() 两种情况讨论函数的单调性,判断函数的零点个数,当
两种情况讨论函数的单调性,判断函数的零点个数,当![]() 时,
时,![]() ,
,
设![]() ,再次求函数的导数,判断函数的单调性和最小值,讨论求函数的零点个数.
,再次求函数的导数,判断函数的单调性和最小值,讨论求函数的零点个数.
解:(1)![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴当![]() 时,
时,![]() .故
.故![]() ,从而
,从而![]() .
.
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() ,从而
,从而![]() ;
;
当![]() 时,
时,![]() ,从而
,从而![]() ;
;
当![]() 时,
时,![]() ,从而
,从而![]() .
.
(2)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
∴当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,∴
,∴![]() 有
有![]() 个零点.
个零点.
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
∴![]() 在上
在上![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴![]() .
.
设![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴
.∴![]() .
.
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;故
;故![]() 有
有![]() 个零点.
个零点.
当![]() 时,
时,![]() ,故
,故![]() 有
有![]() 个零点.
个零点.
当![]() 时,
时,![]() ,即
,即![]() ,
,
又当![]() 时,
时,![]() ;由(1)知
;由(1)知![]() ,故
,故![]() 有
有![]() 个零点.
个零点.
当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点;当
个零点;当![]() 且
且![]() 时,
时,![]() 有
有![]() 个零点.
个零点.


科目:高中数学 来源: 题型:
【题目】某中学组织高二年级开展对某品牌西瓜市场调研活动.两名同学经过了解得知此品牌西瓜,不仅便宜而且口味还不错,并且每日的销售量y(单位:千克)与销售价格x(元/千克)满足关系式:![]() ,其中
,其中![]() ,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()

A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
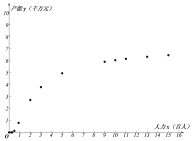
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为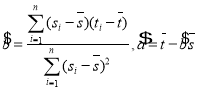 ,(说明:
,(说明:![]() 的导函数为
的导函数为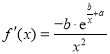 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
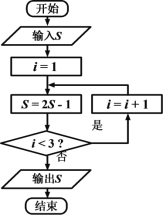
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为曲线
的极坐标方程为曲线![]() .
.
(Ⅰ)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求直线![]() 和曲线
和曲线![]() 的两个交点到点
的两个交点到点![]() 的距离的和与积.
的距离的和与积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com