[题目]“猜想是指对于每一个正整数,若为偶数,则让它变成;若为奇数,则让它变成.如此循环,最终都会变成,若数字按照以上的规则进行变换,则变换次数为偶数的频率是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】“猜想”是指对于每一个正整数,若为偶数,则让它变成;若为奇数,则让它变成.如此循环,最终都会变成,若数字按照以上的规则进行变换,则变换次数为偶数的频率是( )

A.B.C.D.

【答案】B

【解析】

分别对数字按照若为偶数,则让它变成;若为奇数,则让它变成.如此循环,最终都会变成,进行计算,即可求得变换次数为偶数的频率.

①当,第次运算为:,第次运算为:,运算次数为;

②当,第次运算为:,第次运算为:,

第次运算为:,第次运算为:,

第次运算为:,运算次数为;

③当,第次运算为:,第次运算为:,

第次运算为:,第次运算为:,

第次运算为:,第次运算为:,运算次数为;

④当,第次运算为:,第次运算为:,

第次运算为:,第次运算为:,

根据③可知当,还需要次运算,运算次数为;

⑤当,根据②可知当,还需要次运算,运算次数为;

故数字按照以上的规则进行变换,变换次数为偶数的为次

变换次数为偶数的频率为:.

故选:B.

练习册系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知圆：，过且与圆相切的动圆圆心为.

（1）求点的轨迹的方程；

（2）已知过点的两直线和互相垂直，且直线交曲线于，两点，直线交曲线于，两点（，，，为不同的四个点），求四边形的面积的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将三棱锥与拼接得到如图所示的多面体，其中，，，分别为，，，的中点，.

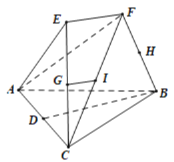
（1）当点在直线上时，证明：平面；

（2）若与均为面积为的等边三角形，求该多面体体积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在极坐标系中，曲线的极坐标方程为，以极点为原点，以极轴所在直线为轴建立直角坐标系，曲线分别与轴正半轴和轴正半轴交于点，，为直线上任意一点，点在射线上运动，且．

（1）求曲线的直角坐标方程；

（2）求点轨迹围成的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，椭圆E：（）的长轴长为4，左准线l的方程为.

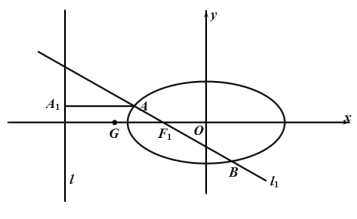
（1）求椭圆的标准方程；

（2）直线过椭圆E的左焦点，且与椭圆E交于A，B两点.

①若，求直线的方程；

②过A作左准线l的垂线，垂足为，点，求证：，B，G三点共线.

查看答案和解析>>

科目：高中数学 来源： 题型：

（1）求曲线的直角坐标方程；

（2）求点轨迹围成的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某品牌汽车4S店，对该品牌旗下的A型、B型、C型汽车进行维修保养，汽车4S店记录了100辆该品牌三种类型汽车的维修情况，整理得下表：

车型	A型	B型	C型
频数	20	40	40

假设该店采用分层抽样的方法从上述维修的100辆该品牌三种类型汽车中随机取10辆进行问卷回访．

（1）求A型、B型、C型各车型汽车抽取的数目；

（2）维修结束后这100辆汽车的司机采用“100分制”打分的方式表示对4S店的满意度，按照大于等于80为优秀，小于80为合格，得到如下列联表：

	优秀	合格	合计
男司机	10	38	48
女司机	25	27	52
合计	35	65	100

问能否在犯错误概率不超过0.01的前提下认为司机对4S店满意度与性别有关系？请说明原因．

（参考公式：）

附表：

	0.100	0.050	0.010	0.001
K	2.706	3.841	6.635	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《九章算术》中《方田》章有弧田面积计算问题，计算术曰：以弦乘矢，矢又自乘，并之，二而一.其大意是，弧田面积计算公式为：弧田面积（弦乘矢+矢乘矢），弧田是由圆弧（简称为弧田的弧）和以圆弧的端点为端点的线段（简称（弧田的弦）围成的平面图形，公式中“弦”指的是弧田的弦长，“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田，其弦长等于，其弧所在圆为圆，若用上述弧田面积计算公式计算得该弧田的面积为，则（）