
 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
, 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值. 的分布列, (2)求
的分布列, (2)求 的数学期望.
的数学期望.科目:高中数学 来源:不详 题型:解答题
 (假定每次通过率相同)
(假定每次通过率相同)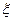 的分布列及数学期望;
的分布列及数学期望; )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为
都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为| 到站的时刻 | 8:10 9:10 | 8:30 9:30 | 8:50 9:50 |
| 概率 |  |  |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com