
【题目】为了调查观众对某热播电视剧的喜爱程度,某电视台在甲、乙两地各随机抽取了8名观众作问卷调查,得分统计结果如图所示:
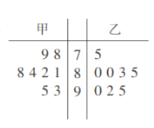
(1)计算甲、乙两地被抽取的观众问卷的平均得分;
(2)计算甲、乙两地被抽取的观众问卷得分的方差;
(3)若从甲地被抽取的8名观众中再邀请2名进行深入调研,求这2名观众中恰有1人的问卷调查成绩在90分以上的概率.
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中, ![]() ,
, ![]() 与
与![]() 交于
交于![]() 点,现将
点,现将![]() 沿
沿![]() 折起得到三棱锥
折起得到三棱锥![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
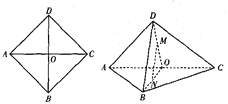
(1)求证: ![]() ;
;
(2)若三棱锥![]() 的最大体积为
的最大体积为![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() ,且二面角
,且二面角![]() 为锐角时,求二面角
为锐角时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 右支上的一点
右支上的一点![]() ,经过点
,经过点![]() 的直线与双曲线
的直线与双曲线![]() 的两条渐近线分别相交于
的两条渐近线分别相交于![]() ,
,![]() 两点.若点
两点.若点![]() ,
,![]() 分别位于第一,四象限,
分别位于第一,四象限,![]() 为坐标原点.当
为坐标原点.当![]() 时,
时,![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费x(单位:万元)对年销量y(单位:吨)和年利润(单位:万元)的影响.对近6宣传费xi和年销售量yi(i=1,2,3,4,5,6)的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费x(万元)与年销售量y(吨)之间近似满足关系式y=axb(a,b>0),即lny=blnx+lna.,对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于20吨的概率.
(Ⅱ)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ) 若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),则2019年该公司应该投入多少宣传费才能使利润最大?(其中
(万元),假定该产品产销平衡(即生产的产品都能卖掉),则2019年该公司应该投入多少宣传费才能使利润最大?(其中![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为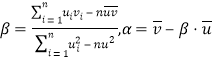
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与![]() 均为等边三角形,点
均为等边三角形,点![]() 为
为![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)试问在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
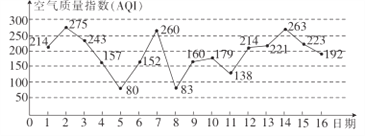
(1)若该人到达后停留![]() 天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
(2)若该人到达后停留3天(到达当日算1天〉,设![]() 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com