
分析 (Ⅰ)求出f(x)的分段函数的解析式,从而求出函数的最大值和最小值即可;
(Ⅱ)通过讨论a的范围,得到$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$的表达式,从而求出a的范围即可.
解答 解:(Ⅰ)∵a=-1,
∴f(x)=x|x+2|+5=$\left\{\begin{array}{l}{{-x}^{2}-2x+5,(-3≤x<-2)}\\{{x}^{2}+2x+5,(-2≤x≤0)}\end{array}\right.$,
x∈[-2,0]时,4≤f(x)≤5,
x∈[-3,-2]时,2≤f(x)≤5,
∴f(x)min=f(-3)=2,f(x)max=f(0)=5;
(Ⅱ)∵f(x)=$\left\{\begin{array}{l}{{x}^{2}-2ax{+a}^{2}-4a,(x≥2a)}\\{{-x}^{2}+2ax{+a}^{2}-4a(x<2a)}\end{array}\right.$,
①若a>0,∵方程f(x)=0有3个不相等的实根,
故x<2a时,方程f(x)=-x2+2ax+a2-4a=0有2个不相等的实根,
x≥2a时,方程f(x)=x2-2ax+a2-4a=0有1个不相等的实根,
∴$\left\{\begin{array}{l}{{4a}^{2}+4{(a}^{2}-4a)>0}\\{{a}^{2}-4a<0}\end{array}\right.$,解得:2<a<4,
不妨设x1<x2<x3,则x1+x2=2a,x1x2=-a2+4a,x3=a+2$\sqrt{a}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$=$\frac{2a}{a(4-a)}$+$\frac{a-2\sqrt{a}}{{a}^{2}-4a}$=-$\frac{1}{a-2\sqrt{a}}$>$\frac{1+\sqrt{2}}{2}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$的范围是($\frac{1+\sqrt{2}}{2}$,+∞),
②若a<0,当x>2a时,方程f(x)=x2-2ax+a2-4a=0的判别式小于0,
不符合题意;
③a=0时,显然不和题意,
故$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$的范围是($\frac{1+\sqrt{2}}{2}$,+∞).
点评 本题考查了分段函数问题,考查二次函数的性质以及分类讨论思想,是一道中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 0或4 | C. | -1或$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
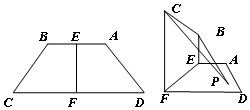 如图,在等腰梯形ABCD中,CD=2AB=2EF=2a,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得平面BEFC⊥平面ADFE.若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1,θ2(θ1,θ2均不为0).若θ1=θ2,则动点P的轨迹围成的图形的面积为( )
如图,在等腰梯形ABCD中,CD=2AB=2EF=2a,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得平面BEFC⊥平面ADFE.若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1,θ2(θ1,θ2均不为0).若θ1=θ2,则动点P的轨迹围成的图形的面积为( )| A. | $\frac{1}{4}{a^2}$ | B. | $\frac{4}{9}{a^2}$ | C. | $\frac{1}{4}π{a^2}$ | D. | $\frac{4}{9}π{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
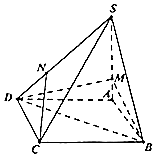 如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1,-4) | B. | (-2,-1,-4) | C. | (2,-1,4) | D. | (2,1,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com