
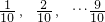 中任取的三个数,求a,b,c能构成三角形三边长的概率;
中任取的三个数,求a,b,c能构成三角形三边长的概率;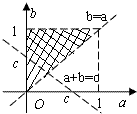 解:(1)若a,b,c能构成三角形,则
解:(1)若a,b,c能构成三角形,则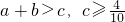 .
. 时,
时,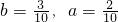 .共1种;
.共1种;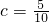 时.
时. .共2种;
.共2种; 时,有3+1=4种;
时,有3+1=4种;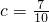 时,有4+2=6种;
时,有4+2=6种;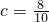 时,有5+3+1=9种;
时,有5+3+1=9种; 时,有6+4+2=12种.
时,有6+4+2=12种.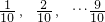 中任取的三个数a,b,c(a<b<c)的种数:
中任取的三个数a,b,c(a<b<c)的种数: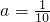 ,
,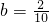 ,则
,则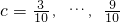 ,有7种;
,有7种;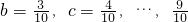 ,有6种;
,有6种;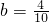 ,
,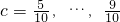 ,有5种;…;
,有5种;…; 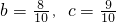 ,有1种.
,有1种.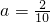 时,有6+5+4+3+2+1=21种;
时,有6+5+4+3+2+1=21种;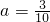 时,有5+4+3+2+1=15种;
时,有5+4+3+2+1=15种;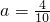 时,有4+3+2+1=10种;
时,有4+3+2+1=10种;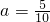 时,有3+2+1=6种;
时,有3+2+1=6种;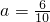 时,有2+1=3种;
时,有2+1=3种;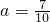 时,有1种.这时共有28+21+15+10+6+3+1=84种.
时,有1种.这时共有28+21+15+10+6+3+1=84种.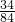 =
=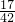 .
.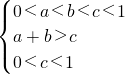 .
. ,于是所要求的概率为
,于是所要求的概率为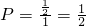 .
.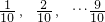 中任取的三个数a,b,c(a<b<c)的种数,利用古典概型的概率公式解之即可;
中任取的三个数a,b,c(a<b<c)的种数,利用古典概型的概率公式解之即可;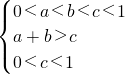 ,在坐标系aOb内画出满足以上条件的区域,由几何概型的计算方法可求出所求.
,在坐标系aOb内画出满足以上条件的区域,由几何概型的计算方法可求出所求.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com