
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
【答案】(1)![]() 人,
人,![]() ,直方图见解析;(2)
,直方图见解析;(2)![]() 人、
人、![]() 人、
人、![]() 人;(3)
人;(3)![]() .
.
【解析】
(1)由频率分布直方图能求出第![]() 组的频数,第
组的频数,第![]() 组的频率,从而完成频率分布直方图.
组的频率,从而完成频率分布直方图.
(2)根据第![]() 组的频数计算频率,利用各层的比例,能求出第
组的频数计算频率,利用各层的比例,能求出第![]() 组分别抽取进入第二轮面试的人数.
组分别抽取进入第二轮面试的人数.
(3)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,利用列举法能出所有基本事件及满足条件的基本事件的个数,利用古典概型求得概率.
,利用列举法能出所有基本事件及满足条件的基本事件的个数,利用古典概型求得概率.
(1)①由题可知,第2组的频数为![]() 人,
人,
②第![]() 组的频率为
组的频率为![]() ,
,
频率分布直方图如图所示,
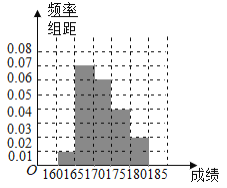
(2)因为第![]() 组共有
组共有![]() 名学生,
名学生,
所以利用分层抽样在![]() 名学生中取
名学生中取![]() 名学生进入第二轮面试,每组抽取的人数分别为:
名学生进入第二轮面试,每组抽取的人数分别为:
第![]() 组:
组: ![]() 人,
人,
第![]() 组:
组:![]() 人,
人,
第![]() 组:
组:![]() 人,
人,
所以第![]() 组分别抽取
组分别抽取![]() 人、
人、![]() 人、
人、![]() 人进入第二轮面试.
人进入第二轮面试.
(3)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,
,
则从这六位同学中抽取两位同学有![]() 种选法,分别为:
种选法,分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其中第![]() 组的
组的![]() 位同学
位同学![]() 中至少有一位同学入选的有
中至少有一位同学入选的有![]() 种,分别为:
种,分别为:![]() ,
,![]() ,
,![]() ,
,
∴第![]() 组至少有一名学生被
组至少有一名学生被![]() 考官面试的概率为
考官面试的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的方程为 ![]() ,点
,点 ![]() ,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)求曲线C的直角坐标方程及点R的直角坐标;
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线![]() 的极坐标方程为
的极坐标方程为![]() ,圆C的参数方程为
,圆C的参数方程为![]() ,
,
(1)求直线![]() 被圆C所截得的弦长;
被圆C所截得的弦长;
(2)已知点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆所相交于
与圆所相交于![]() 不同的两点,求
不同的两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对某种食材营养价值的认识程度,某档健康养生电视节目组织![]() 名营养专家和
名营养专家和![]() 名现场观众各组成一个评分小组,给食材的营养价值打分(十分制).下面是两个小组的打分数据:
名现场观众各组成一个评分小组,给食材的营养价值打分(十分制).下面是两个小组的打分数据:
第一小组 |
|
|
|
|
|
|
|
|
第二小组 |
|
|
|
|
|
|
|
|

(1)求第一小组数据的中位数与平均数,用这两个数字特征中的哪一种来描述第一小组打分的情况更合适?说明你的理由.
(2)你能否判断第一小组与第二小组哪一个更像是由营养专家组成的吗?请比较数字特征并说明理由.
(3)节目组收集了烹饪该食材的加热时间:(单位:![]() )与其营养成分保留百分比
)与其营养成分保留百分比![]() 的有关数据:
的有关数据:
食材的加热时间 |
|
|
|
|
|
|
营养成分保留百分比 |
|
|
|
|
|
|
在答题卡上画出散点图,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),并说明回归方程中斜率
),并说明回归方程中斜率![]() 的含义.
的含义.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com