
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展,下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
参考公式: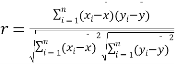 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() ( 其中
( 其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(Ⅰ)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.|.
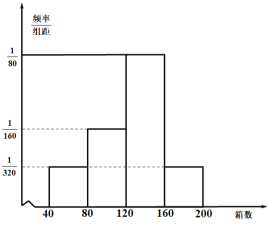
(Ⅱ)据统计,10月份的连续16天中该农户每天为甲地配送的该新奇水果的箱数的频率分布直方图如图所示.
(i)若从箱数在![]() 内的天数中随机抽取2天,估计恰有1天的水果箱数在
内的天数中随机抽取2天,估计恰有1天的水果箱数在![]() 内的概率;
内的概率;
(ⅱ)求这16天该农户每天为甲地配送的该新奇水果的箱数的平均值.(每组用该组区间的中点值作代表)
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为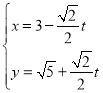 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
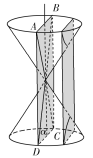
【题目】古希腊数学家阿波罗尼斯在他的著作《圆锥曲线论》中记载了用平面切割圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径均为1,母线长均为3,记过圆锥轴的平面![]() 为平面
为平面![]() (
(![]() 与两个圆锥侧面的交线为
与两个圆锥侧面的交线为![]() ),用平行于
),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的交线即双曲线
的平面截圆锥,该平面与两个圆锥侧面的交线即双曲线![]() 的一部分,且双曲线
的一部分,且双曲线![]() 的两条渐近线分别平行于
的两条渐近线分别平行于![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为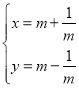 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆短轴端点,若
为椭圆短轴端点,若![]() 为直角三角形且周长为
为直角三角形且周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() ,
,![]() 斜率的乘积为
斜率的乘积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com