练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为${60°}，|{\overrightarrow a}|=2，|{\overrightarrow b}|=6$，则$2\overrightarrow a-\overrightarrow b$在$\overrightarrow a$方向上的投影为1．

    分析 由已知求出$（2\overrightarrow{a}-\overrightarrow{b}）•\overrightarrow{a}$，然后代入投影概念得答案．

    解答 解：∵向量$\overrightarrow a$与$\overrightarrow b$的夹角为${60°}，|{\overrightarrow a}|=2，|{\overrightarrow b}|=6$，
    ∴$（2\overrightarrow{a}-\overrightarrow{b}）•\overrightarrow{a}=2|\overrightarrow{a}{|}^{2}-\overrightarrow{a}•\overrightarrow{b}$=$2×{2}^{2}-2×6×\frac{1}{2}=2$，
    ∴$2\overrightarrow a-\overrightarrow b$在$\overrightarrow a$方向上的投影为$\frac{（2\overrightarrow{a}-\overrightarrow{b}）•\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{2}{2}=1$．
    故答案为：1．

    点评 本题考查平面向量的数量积运算，考查了向量在向量方向上的投影的概念，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．新定义运算：$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则满足$|\begin{array}{l}{i}&{z}\\{-1}&{z}\end{array}|$=2的复数z是1-i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（1）将二次函数h（x）=x2的图象先向右平移1个单位，再向下平移2个单位得到函数f（x）的图象，写出函数f（x）的解析式，并求出x∈[0，4]时函数f（x）的值域．
    （2）求f（x）=x2-2ax-1在区间[0，2]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设min{p，q}表示p，q两者中的较小者，若函数f（x）=min{3-x，log2x}，则f（x）的最大值为2，满足$f（x）＜\frac{1}{2}$的集合为{x|0＜x＜$\sqrt{2}$或x＞$\frac{5}{2}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．（1）计算：$2{log_5}10+{log_5}0.25+{2^{{{log}_2}3}}$
    （2）计算：${（{5\frac{1}{16}}）^{0.5}}+{（{-1}）^{-1}}÷{0.75^{-2}}+{（{2\frac{10}{27}}）^{-\frac{2}{3}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

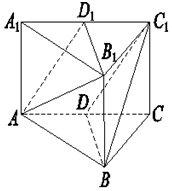    2．如图所示，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1中点
    （1）求证：BC1∥平面AB1D1
    （2）求证：平面AB1D1∥平面C1BD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，长轴长为4．
    （1）求椭圆C的方程；
    （2）设动直线l1：y=kx+m与椭圆C有且只有一个公共点P，过右焦点F作直线l2与直线l1交与点Q，且$\overrightarrow{PF}$•$\overrightarrow{FQ}$=0．求证：点Q在定直线上，并求出定直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）（x∈R）是奇函数，且当x＞0时，f（x）=2x-1．
    （1）求函数f（x）的解析式；     
    （2）求f（f（-2））的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线为正方形OABC的边OA，OC所在直线，点B为该双曲线的焦点，若正方形OABC的边长为2，则a=（　　）
    A．1B．2C．$\frac{1}{2}$D．4

    查看答案和解析>>

    同步练习册答案