练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于命题：存在一个常数，使得不等式对任意正数，恒成立.

    （1）试给出这个常数的值；

    （2）在（1）所得结论的条件下证明命题；

    （3）对于上述命题，某同学正确地猜想了命题：“存在一个常数，使得不等式对任意正数，，恒成立．”观察命题与命题的规律，请猜想与正数，，，相关的命题．

    【答案】(1) ;(2)详见解析;(3)详见解析.

    【解析】试题分析：（1）取特值，定常数的值；（2）利用分析法证明命题P;(3).猜想结论：存在一个常数，使得不等式

    对任意正数，，，恒成立.

    试题解析：

    （1）令得：，故；

    （2）先证明.

    ∵，，要证上式，只要证，

    即证 即证，这显然成立.

    ∴.

    再证明.

    ∵，，要证上式，只要证，

    即证 即证，这显然成立.

    ∴.

    （3）猜想结论：存在一个常数，使得不等式

    对任意正数，，，恒成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的短轴长为，离心率．

    （1）求椭圆的标准方程；

    （2）若分别是椭圆的左、右焦点，过的直线与椭圆交于不同的两点，求的内切圆半径的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）是定义在R上的偶函数，且对任意的x∈R，都有f（x+2）=f（x）．当0≤x≤1时，f（x）=x2．若直线y=x+a与函数y=f（x）的图象有两个不同的公共点，则实数a的值为（　　）

    A. n（n∈Z） B. 2n（n∈Z）

    C. 2n或（n∈Z） D. n或（n∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝|2x－1|＋|2x－a|＋a，x∈R.

    (1)当a＝3时，求不等式f(x)>7的解集；

    (2)对任意x∈R恒有f(x)≥3，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

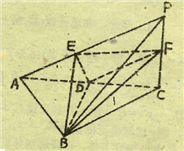
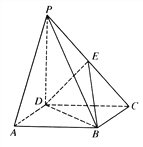
    【题目】已知三棱锥P—ABC中，PC底面ABC，AB=BC，D、F分别为AC、PC的中点，DEAP于E。（1）求证：AP平面BDE；（2）求证：平面BDE平面BDF；（3）若AE：EP=1：2，求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （Ⅰ）若，求的极值；

    （Ⅱ）若对于任意的，，都有，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的平面图形中，ABCD是边长为2的正方形，△HDA和△GDC都是以D为直角顶点的等腰直角三角形，点E是线段GC的中点．现将△HDA和△GDC分别沿着DA，DC翻折，直到点H和G重合为点P．连接PB，得如图的四棱锥．

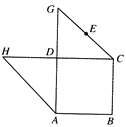
    （Ⅰ）求证：PA//平面EBD；

    （Ⅱ）求二面角大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：

    td style="width:16.2pt; padding:3.75pt 5.4pt; vertical-align:middle">

    男

    女

    15

    6

    5

    4

    16

    3

    5

    8

    8

    2

    17

    2

    3

    6

    8

    8

    8

    6

    5

    18

    5

    7

    19

    2

    3

    （Ⅰ）计算上线考生中抽取的男生成绩的方差；（结果精确到小数点后一位）

    （Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车间20名工人年龄数据如下表：

    年龄（岁）

    19

    24

    26

    30

    34

    35

    40

    合计

    工人数（人）

    1

    3

    3

    5

    4

    3

    1

    20

    （1）求这20名工人年龄的众数与平均数；

    （2）以十位数为茎，个位数为叶，作出这20名工人年龄的茎叶图；

    （3）从年龄在24和26的工人中随机抽取2人，求这2人均是24岁的概率.

    查看答案和解析>>

    同步练习册答案