
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg)其频率分布直方图如下:

(1) 记![]() 表示事件“旧养殖法的箱产量低于50kg”,估计
表示事件“旧养殖法的箱产量低于50kg”,估计![]() 的概率;
的概率;
(2)填写下面联表,并根据列联表判断是否有![]() %的把握认为箱产量与养殖方法有关:
%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【答案】(1)![]() ,(2)有99%的把握认为箱产量与养殖方法有关,(3)新养殖法优于旧养殖法.
,(2)有99%的把握认为箱产量与养殖方法有关,(3)新养殖法优于旧养殖法.
【解析】分析:(1)根据旧养殖法的频率分布直方图的性质可估计![]() 的概率;(2)由的频率分布直方图可以将列联表补全,进而利用公式可得
的概率;(2)由的频率分布直方图可以将列联表补全,进而利用公式可得![]() ,与附表比较即可得结论;(3)由频率分布直方图计算新养殖法箱产量的平均数,比较即可得结论.
,与附表比较即可得结论;(3)由频率分布直方图计算新养殖法箱产量的平均数,比较即可得结论.
详解:(1) 旧养殖法的箱产量低于![]() 的频率为
的频率为![]()
因此,事件![]() 的概率估计值为
的概率估计值为![]()
(2)根据箱产量的频率分布直方图得列联表

![]()
由于![]() ,故有
,故有![]() %的把握认为箱产量与养殖方法有关.
%的把握认为箱产量与养殖方法有关.
(3)箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在![]() 到
到![]() 之间,旧养殖法的箱产量平均值(或中位数)在
之间,旧养殖法的箱产量平均值(或中位数)在![]() 到
到![]() 之间,且新养殖法的箱产量分布程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.
之间,且新养殖法的箱产量分布程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:对于任意的实数
满足:对于任意的实数![]() 都有
都有![]() 成立,且当
成立,且当![]() 时,
时, ![]() 恒成立,且
恒成立,且![]() 是一个给定的正整数).
是一个给定的正整数).
(1)判断函数![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)判断并证明![]() 的单调性;若函数
的单调性;若函数![]() 在
在![]() 上总有
上总有![]() 成立,试确定
成立,试确定![]() 应满足的条件;
应满足的条件;
(3)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有
的子集个数有![]() 个;②定义在
个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.
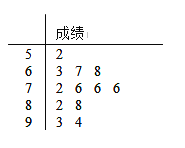
(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人.
①记![]() 表示选取4人的成绩的平均数,求
表示选取4人的成绩的平均数,求![]() ;
;
②记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布和数学期望.
的分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com