
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)试写出![]() ;
;
(2)设![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)求出数列![]() 的前
的前![]() 项和为
项和为![]() 及数列
及数列![]() 的通项公式.
的通项公式.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3},集合B={x|a+1<x<6a﹣1},其中a∈R.
(1)写出集合A的所有真子集;
(2)若A∩B={3},求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,边AB、AD的长分别为2,1,若M,N分别是边BC、CD上的点,且满足 ![]() =
= ![]() =λ.
=λ. 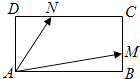
(1)当λ= ![]() 时,求向量
时,求向量 ![]() 和
和 ![]() 夹角的余弦值;
夹角的余弦值;
(2)求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量![]() 的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
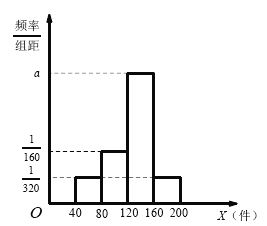
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每
趟最多只能装载40 件货物,满载发车,否则不发车。若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元。为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,过
的焦点,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() 为
为![]() 中点,点
中点,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)过![]() 分别作
分别作![]() 的两条切线
的两条切线![]() ,
, ![]() .请选择
.请选择![]() 轴中的一条,比较
轴中的一条,比较![]() 到该轴的距离.
到该轴的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个结论:
①在△ABC中,若sinA>sinB,则必有cosA<cosB;
②在△ABC中,若a,b,c成等比数列,则角B的取值范围为 ![]() ;
;
③等比数列{an}中,若a3=2,a7=8,则a5=±4;
④等差数列{an}的前n项和为Sn , S10<0且S11=0,满足Sn≥Sk对n∈N*恒成立,则正整数k构成集合为{5,6}
⑤若关于x的不等式(a2﹣1)x2﹣(a﹣1)x﹣1<0的解集为R,则a的取值范围为 ![]() .
.
其中正确结论的序号是 . (填上所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(m+![]() )(m∈R,且m>0).
)(m∈R,且m>0).
(1)求函数f(x)的定义域;
(2)若函数f(x)在(4,+∞)上单调递增,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com