
已知函数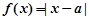 。
。
(1)若 的解集为
的解集为 ,求实数
,求实数 的值。
的值。
(2)当 且
且 时,解关于
时,解关于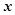 的不等式
的不等式 。
。
(Ⅰ)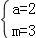 . (Ⅱ)当t=0时,原不等式的解集为R,当t>0时,原不等式的解集为
. (Ⅱ)当t=0时,原不等式的解集为R,当t>0时,原不等式的解集为 .
.
解析试题分析:(Ⅰ)由|x﹣a|≤m得a﹣m≤x≤a+m,
所以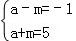 解之得
解之得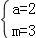 为所求. 4分
为所求. 4分
(Ⅱ)当a=2时,f(x)=|x﹣2|,
所以f(x)+t≥f(x+2t)?|x﹣2+2t|﹣|x﹣2|≤t,①
当t=0时,不等式①恒成立,即x∈R;
当t>0时,不等式
解得x<2﹣2t或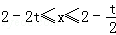 或x∈ϕ,即
或x∈ϕ,即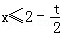 ;
;
综上,当t=0时,原不等式的解集为R,
当t>0时,原不等式的解集为 . 10分
. 10分
考点:本题考查了绝对值不等式的解法及恒成立问题的解法
点评:不等式选讲主要考查绝对值不等式的解法、不等式证明及其应用,要求学生学会从分段函数角度来解绝对值不等式及绝对值不等式的最值问题等,掌握常见的证明不等式的方法如综合法、分析法、数学归纳法等。


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数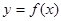 的定义域为
的定义域为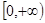 ,且对于任意
,且对于任意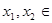
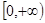 ,存在正实数L,使得
,存在正实数L,使得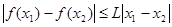 均成立。
均成立。
(1)若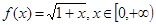 ,求正实数L的取值范围;
,求正实数L的取值范围;
(2)当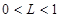 时,正项数列{
时,正项数列{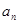 }满足
}满足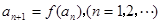
①求证: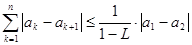 ;
;
②如果令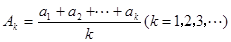 ,求证:
,求证: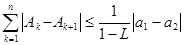 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com