
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=Asin(ωx+)(A>0,ω>0,||< ![]() )的部分图象如图所示:
)的部分图象如图所示: 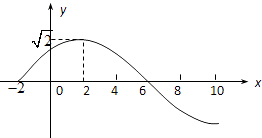
(1)求函数f(x)的解析式;
(2)若g(x)的图象是将f(x)的图象先向右平移1个单位,然后纵坐标不变横坐标缩短到原来的一半得到的,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)当![]() ,是否在折叠后的
,是否在折叠后的![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 点位置,若不存在,说明理由;
点位置,若不存在,说明理由;
(2)设![]() ,问当
,问当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积有最大值?并求出这个最大值.
的体积有最大值?并求出这个最大值.
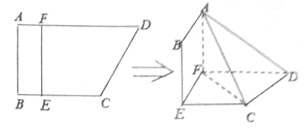
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)在数列![]() 中,对于任意
中,对于任意![]() ,等式
,等式![]()
成立,其中常数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:数列![]() 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式![]() 的解集为
的解集为
![]() ,求b和c的取值范围.
,求b和c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的参数方程为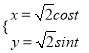 (t为参数)
(t为参数) 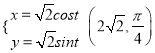 .
.
(1)若曲线C在点(1,1)处的切线为l,求l的极坐标方程;
(2)若点A的极坐标为![]() ,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(Ⅰ)若直线l不经过第二象限,求实数a的取值范围;
(Ⅱ)若直线l与两坐标轴围成的三角形面积等于2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:![]() =
=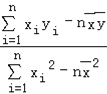 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.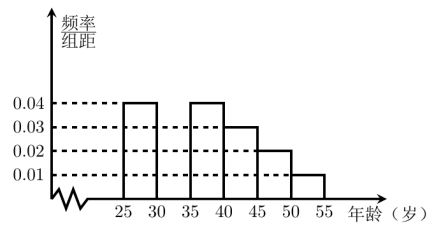
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 ,
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an , 求数列{ ![]() }的前n项和.
}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com