
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
科目:高中数学 来源: 题型:
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六棱锥P﹣ABCDEF中,六边形ABCDEF为正六边形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
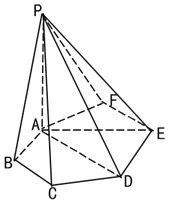
(1)求证:PA⊥平面ABCDEF;
(2)求直线PD与平面PAE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )

A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.
的中点.
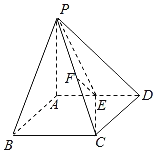
(1)求证:![]() 平面
平面![]() ;
;
(2)点G是线段![]() 上一动点,若
上一动点,若![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,且Sn=n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令![]() (n∈N*),求数列{cn}的前n项和Tn.
(n∈N*),求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学随机抽取部分高一学生调查其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成如图所示的频率分布直方图,其中自主安排学习时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
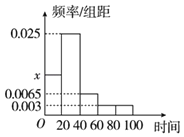
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)从学校全体高一学生中任选![]() 名学生,这
名学生,这![]() 名学生中自主安排学习时间少于
名学生中自主安排学习时间少于![]() 分钟的人数记为
分钟的人数记为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com