
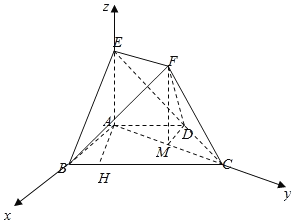
【题目】在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=AE=1,∠ABC=60°,EF=
,AD=AE=1,∠ABC=60°,EF=![]() AC,且EF
AC,且EF![]() AC.
AC.
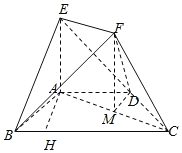
(Ⅰ)证明:AB⊥CF;
(Ⅱ)求二面角B﹣EF﹣D的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)由EA⊥平面ABCD得BA⊥AE.由四边形ABCD为等腰梯形,![]() ,且
,且![]() ,∠ABC=60°,得AB⊥AC,进而推出AB⊥平面ACFE.即可得AB⊥CF.
,∠ABC=60°,得AB⊥AC,进而推出AB⊥平面ACFE.即可得AB⊥CF.
(Ⅱ)以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,求出平面BEF的一个法向量,平面DEF的一个法向量,通过向量的数量积求解二面角的余弦值即可.
(Ⅰ)由题知EA⊥平面ABCD,BA![]() 平面ABCD,∴BA⊥AE.
平面ABCD,∴BA⊥AE.
四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=1,所以BC=2,∠ABC=60°,
,AD=1,所以BC=2,∠ABC=60°,
过点A作AH⊥BC于H,在RT△ABH中,![]() ,∴AB=1,
,∴AB=1,
在△ABC中,AC2=AB2+BC2﹣2ABBCcos60°=3,∴AB2+AC2=BC2,∴AB⊥AC,
且AC∩EA=A,∴AB⊥平面ACFE.又∵CF平面ACFE,∴AB⊥CF.
(Ⅱ)以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,
EF=![]() AC,且EF
AC,且EF![]() AC,AD=AE=1,则
AC,AD=AE=1,则 ,
,
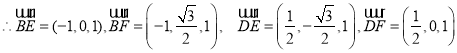
设![]() 为平面BEF的一个法向量,则
为平面BEF的一个法向量,则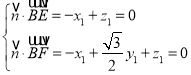 令
令![]() ,得
,得![]() ,
,
设![]() 为平面DEF的一个法向量,则
为平面DEF的一个法向量,则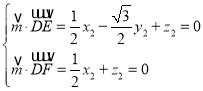 令
令![]() ,得
,得![]() ,
,
∴![]() ,二面角B﹣EF﹣D的余弦值为
,二面角B﹣EF﹣D的余弦值为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】电子计算机诞生于20世纪中叶,是人类最伟大的技术发明之一.计算机利用二进制存储信息,其中最基本单位是“位(bit)”,1位只能存放2种不同的信息:0或l,分别通过电路的断或通实现.“字节(Byte)”是更大的存储单位,1Byte=8bit,因此1字节可存放从00000000(2)至11111111(2)共256种不同的信息.将这256个二进制数中,所有恰有相邻两位数是1其余各位数均是0的所有数相加,则计算结果用十进制表示为
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为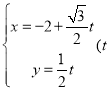 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于点
交于点![]() (不同于原点),与直线
(不同于原点),与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与极轴所在直线交于点
与极轴所在直线交于点![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,右表是对 100 辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
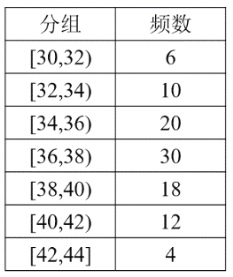
(Ⅰ)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(Ⅱ)用分层抽样的方法从行车里程在区间[38,40)与[40,42)的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在[40,42)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式m-|x-2|≥1,其解集为[0,4].
(1)求m的值;
(2)若a,b均为正实数,且满足a+b=m,求a2+b2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识,高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人,女生200人;文科班有男生100人,女生300人.现按男、女用分层抽样从理科生中抽取6人,按男、女分层抽样从文科生中抽取4人,组成环境保护兴趣小组,再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.
(1)设事件![]() 为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件
为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示抽取的4人中文科女生的人数,求
表示抽取的4人中文科女生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com