
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 | 2004 | 2006 | 2008 | 2010 | 2012 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
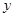 =
=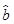 x+
x+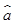
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:解答题
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| | 有关系 | 无关系 | 不知道 |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.
| 组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) |  | 0.9 |
| 第3组 | [35,45) | 27 | 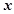 |
| 第4组 | [45,55) |  | 0.36 |
| 第5组 | [55,65) | 3 | 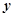 |
 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图: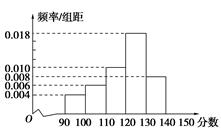
男生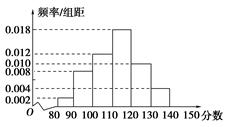
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
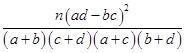 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
| | 轿车A | 轿车B | 轿车C |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间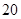 名工人年龄数据如下表:
名工人年龄数据如下表:
| 年龄(岁) | 工人数(人) |
 |  |
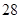 | 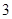 |
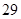 | 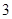 |
 | 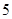 |
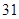 |  |
 | 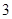 |
 |  |
| 合计 |  |
 名工人年龄的众数与极差;
名工人年龄的众数与极差; 名工人年龄的茎叶图;
名工人年龄的茎叶图; 名工人年龄的方差.
名工人年龄的方差.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下: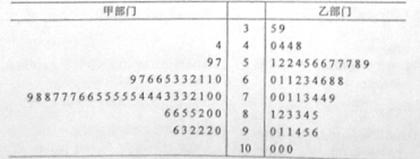
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评优.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:

(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
根据统计资料,在 小镇当某件讯息发布后,
小镇当某件讯息发布后,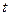 小时之内听到该讯息的人口是全镇人
小时之内听到该讯息的人口是全镇人 口的
口的 ﹪,其中
﹪,其中 是某个大于0的常数,今有某讯息,假设在发布后3小时之内已经
是某个大于0的常数,今有某讯息,假设在发布后3小时之内已经 有70﹪的人口听到该讯息。又设最快要
有70﹪的人口听到该讯息。又设最快要 小时后,有99﹪的人口已听到该讯息,则
小时后,有99﹪的人口已听到该讯息,则 =
= 小时。(保留一位小数)
小时。(保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com