
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
【答案】(I)单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .(II)(i)见解析.(ii)
.(II)(i)见解析.(ii)![]() .
.
【解析】
试题求导数后因式分解根据![]() ,得出
,得出![]() ,根据导数的符号判断函数的单调性,给出单调区间,对
,根据导数的符号判断函数的单调性,给出单调区间,对![]() 求导,根据函数
求导,根据函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,解得
的图象在公共点(x0,y0)处有相同的切线,解得![]() ,根据
,根据![]() 的单调性可知
的单调性可知![]() 在
在![]() 上恒成立,关于x的不等式
上恒成立,关于x的不等式![]() 在区间
在区间![]() 上恒成立,得出
上恒成立,得出![]() ,得
,得![]() ,
,![]() ,
,
求出![]() 的范围,得出
的范围,得出![]() 的范围.
的范围.
试题解析:(I)由![]() ,可得
,可得
![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]() .由
.由![]() ,得
,得![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
所以,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)(i)因为![]() ,由题意知
,由题意知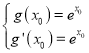 ,
,
所以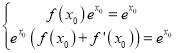 ,解得
,解得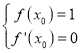 .
.
所以,![]() 在
在![]() 处的导数等于0.
处的导数等于0.
(ii)因为![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() .
.
又因为![]() ,
,![]() ,故
,故![]() 为
为![]() 的极大值点,由(I)知
的极大值点,由(I)知![]() .
.
另一方面,由于![]() ,故
,故![]() ,
,
由(I)知![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
故当![]() 时,
时,![]() 在
在![]() 上恒成立,从而
上恒成立,从而![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,得
,得![]() ,
,![]() .
.
令![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
因为![]() ,
,![]() ,
,![]() ,故
,故![]() 的值域为
的值域为![]() .
.
所以,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,有一张半径为1米的圆形铁皮,工人师傅需要剪一块顶角为锐角的等腰三角形![]() ,不妨设
,不妨设 ![]() ,
, ![]() 边上的高为
边上的高为 ![]() ,圆心为
,圆心为 ![]() ,为了使三角形的面积最大,我们设计了两种方案.
,为了使三角形的面积最大,我们设计了两种方案.

(1)方案1:设 ![]() 为
为 ![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积 ![]() ; 方案2:设
; 方案2:设![]() 的高
的高![]() 为
为![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积![]() ;
;
(2)请从(1)中的两种方案中选择一种,求出![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,![]() ,
,![]() .
.
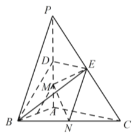
(1)求证:![]() 平面BDE;
平面BDE;
(2)求二面角C-EM-N的正弦值.
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点 ,离心率为
,离心率为![]() .
.![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点.
的一点.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求
,求![]() 的面积;
的面积;
(3)过点![]() 作斜率为
作斜率为![]() 的直线分别交椭圆
的直线分别交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且点
,且点![]() 在线段
在线段![]() 上(不包括端点
上(不包括端点![]() ),直线
),直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 为短轴端点,且
为短轴端点,且![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程,
的方程,
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点![]() ,
,![]() ,且满足
,且满足![]() ?若存在,求出该圆的方程,若不存在,说明理由.
?若存在,求出该圆的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对“2016年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如表:(单位:万人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知从所有参与调查的人中任选1人是“老年人”的概率为![]() .
.
(1)求n的值;
(2)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com