
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且图象关于直线
,且图象关于直线![]() 对称.
对称.
(1)求![]() 的解析式;
的解析式;
(2) 若函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上只有一个交点,求实数
上只有一个交点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
分析:(1)根据二倍角公式以及配角公式将函数化为基本三角函数,再根据正弦函数性质确定![]() 的解析式;(2)先化简
的解析式;(2)先化简![]() ,再同一坐标系中作出y=sin
,再同一坐标系中作出y=sin![]() 和y=a的图象,根据图像确定实数
和y=a的图象,根据图像确定实数![]() 的取值范围.
的取值范围.
详解:(1) f(x)=![]() sinωx·cosωx-cos2ωx+
sinωx·cosωx-cos2ωx+![]() =
=![]() sin2ωx-
sin2ωx-![]() (1+cos2ωx)+
(1+cos2ωx)+![]() =sin
=sin![]() +1.∵ 函数f(x)的最小正周期为π,∴
+1.∵ 函数f(x)的最小正周期为π,∴ ![]() =π,即ω=±1,
=π,即ω=±1,
∴ f(x)=sin![]() +1.
+1.
① 当ω=1时,f(x)=sin![]() +1,∴ f
+1,∴ f![]() =sin
=sin![]() +1不是函数的最大值或最小值,
+1不是函数的最大值或最小值,
∴ 其图象不关于x=![]() 对称,舍去.
对称,舍去.
② 当ω=-1时,f(x)=-sin![]() +1,
+1,
∴ f![]() =-sin
=-sin![]() +1=0是最小值,
+1=0是最小值,
∴ 其图象关于x=![]() 对称.
对称.
故f(x)的解析式为f(x)=1-sin![]() .
.
(2) y=1-f(x)=sin![]() ,在同一坐标系中作出y=sin
,在同一坐标系中作出y=sin![]() 和y=a的图象:
和y=a的图象:

由图可知,直线y=a在a∈![]() 或a=1时,两曲线只有一个交点,∴ a∈
或a=1时,两曲线只有一个交点,∴ a∈![]() 或a=1.
或a=1.


科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A.在等差数列{an}中,若ap+aq=ar+aδ , 则p+q=r+δ
B.已知数列{an}的前n项和为Sn , 若{an}是等比数列,则Sk , S2k﹣Sk , S3k﹣S2k也是等比数列
C.在数列{an}中,若ap+aq=2ar , 则ap , ar , aq成等差数列
D.在数列{an}中,若ap?aq=a ![]() ,则ap , ar , aq成等比数列
,则ap , ar , aq成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面坐标系内,O为坐标原点,向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点M为直线OP上的一个动点.
=(2,1),点M为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求向量
取最小值时,求向量 ![]() 的坐标;
的坐标;
(2)在点M满足(I)的条件下,求∠AMB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,已知
上的偶函数,已知![]() 时,
时,![]() .
.

(1)画出偶函数![]() 的图像;
的图像;
(2)指出函数![]() 的单调递增区间及值域;
的单调递增区间及值域;
(3)若直线![]() 与函数
与函数![]() 恰有
恰有![]() 个交点,求
个交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 由经验得知,在某商场付款处排队等候付款的人数及概率如下表
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex与g(x)=ax+b的图象交于P(x1 , y1),Q(x2 , y2)两点. (Ⅰ)求函数h(x)=f(x)﹣g(x)的最小值;
(Ⅱ)且PQ的中点为M(x0 , y0),求证:f(x0)<a<y0 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2. 表1
停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
频数 | 26 | a | b | 8 | 2 |
表2
平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
已知表1数据的中位数估计值为26,回答以下问题.
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程 ![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1 , y1),(x2 , y2),…,(xn , yn),其回归直线 ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为  ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 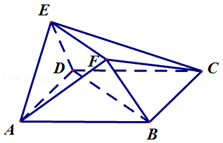
(I)证明:AE⊥CD
(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com