
����Ŀ�����ض�ͬʱ��A��B��C������ͬ�������ڵ�ij����Ʒ���г�����⣬�Ӹ��������ڴ�����Ʒ������(��λ����)�����ʾ��������Ա�÷ֲ�����ķ�������Щ��Ʒ�й���ȡ6����Ʒ���м�⣮
���� | A | B | C |
���� | 50 | 150 | 100 |
��1������6����Ʒ������A��B��C��������Ʒ��������
��2��������6����Ʒ�������ȡ2�������������н�һ����⣬����2����Ʒ������ͬ�����ĸ��ʣ�
���𰸡���1��A,B,C�ֱ���![]() ����2��
����2��![]() .
.
��������
��1�����ݷֲ���������ʼ��ɵó���ȡ���������Ը�������Ʒ��������
��2����6������A��B��C������������Ʒ�ֱ�Ϊ��A��B1��B2��B3��C1��C2.д����ȡ����2����Ʒ���ɵ����л����¼������ҳ���ȡ����2����Ʒ������ͬ���������Ļ����¼������ݹŵ���͵Ĺ�ʽ�������.
(1)��Ϊ���������������еĸ������ı���
![]() ��
��![]() �����������а������������ĸ��������ֱ��ǣ�50��
�����������а������������ĸ��������ֱ��ǣ�50��![]() ��1��150��
��1��150��![]() ��3��100��
��3��100��![]() ��2.
��2.
����A��B��C������������Ʒ��ѡȡ�ļ����ֱ���1��3��2.
(2)��6������A��B��C������������Ʒ�ֱ�Ϊ��A��B1��B2��B3��C1��C2.���ȡ����2����Ʒ���ɵ����л����¼�Ϊ��
{A��B1}��{A��B2}��{A��B3}��{A��C1}��{A��C2}��{B1��B2}��{B1��B3}��{B1��C1}��{B1��C2}��{B2��B3}{B2��C1}��{B2��C2}��{B3��C1}��{B3��C2}��{C1��C2}����15����
ÿ����Ʒ���鵽�Ļ�����ȣ������Щ�����¼��ij����ǵȿ��ܵģ�
���¼�DΪ����ȡ����2����Ʒ������ͬ��������
���¼�D�����Ļ����¼���{B1��B2}��{B1��B3}��{B2��B3}��{C1��C2}����4����
����P(D)��![]() ������2����Ʒ������ͬ�����ĸ���Ϊ
������2����Ʒ������ͬ�����ĸ���Ϊ![]() .
.


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() .
.
��1����![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �����ߵķ��̣�
�����ߵķ��̣�
��2����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ax2+bx+c��a��0������������f��x+1��-f��x��=2x��x��R������f��0��=1��
������f��x���Ľ���ʽ��
����x��0ʱ��f��x����mx-3���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ��������Ϊ
��������Ϊ![]() ��������
��������![]() ����
����![]() ������
������![]() ����
Ϊ����![]() �Ķ�����
�Ķ�����![]() ʱ��
ʱ��![]() ����������
����������![]() ����
Ϊ����![]() �ġ�ת�۵㡱����֪����
�ġ�ת�۵㡱����֪����![]() ������
������![]() �ϴ���һ����ת�۵㡱����
�ϴ���һ����ת�۵㡱����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ��������ͬ����㣬��
��������ͬ����㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ f��x������x��1��ex��ax2��![]() ��
��
(1)��![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
(2)��![]() ��
��![]() ��ȡ�ü���ֵ����
��ȡ�ü���ֵ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ԲE��![]() 1��a��b��0����һ����P��ԲO��x2+y2��b2����������PA��PB���е�ֱ���A��B��ֱ��AB�ֱ���x�ᣬy�ύ�ڵ�M��N��OΪ����ԭ�㣩��
1��a��b��0����һ����P��ԲO��x2+y2��b2����������PA��PB���е�ֱ���A��B��ֱ��AB�ֱ���x�ᣬy�ύ�ڵ�M��N��OΪ����ԭ�㣩��

��1��������ԲE�ϴ��ڵ�P������PA��PB������ԲE�������ʵ�ȡֵ��Χ��
��2����֤������ԲE�ڣ�����һ��C����|CO|��|CA|��|CP|��|CB|��
��3������ԲE�Ķ��᳤Ϊ2����MON�������СֵΪ![]() ������ԲE�ķ��̣�
������ԲE�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֵ���Ʒ��С��Ϻ�ļ��ڣ�С��Ϻ���������������ǡ�������ҹ�����ҹ�����.�ھ�������г��£�������С��Ϻ����ռ����ȫ���İ�ڽ�ɽ������ij�����������С��Ϻ����ͳ�����±���
��� | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 | 6 |
����� | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
��1�����ݱ������ݣ�����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2���������Իع鷽��Ԥ��2019��õ���ũ��Ʒ�������.
��������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��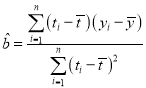 ��
��![]() .���ο����ݣ�
.���ο����ݣ�![]() ������������С�������λ��.
������������С�������λ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ(1)��μ�У���ᄎ��ѧ���ijɼ��ľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���ܵ���ͬ�̶ȵ��ƻ������ɼ��������£��ݴ˽���������⣺

(1)���һ(1)��μ�У���ᄎ����������������[80,90)֮���Ƶ����������Ƶ�ʷֲ�ֱ��ͼ��[80,90)��ľ��εĸߣ�
(2)��Ҫ�ӷ�����[80,100]֮���ѧ������ѡ2�˽���ij���о�����������1�˷�����[90,100]֮��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com