设所求点为
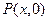
,于是有
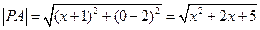
,
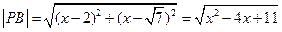
,
由
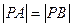
得
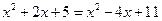
,
解得
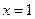
.
所以,所求点为
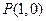
,且
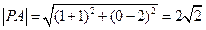
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知直线l经过两条直线l
1:x+2y=0与l
2:3x-4y-10=0的交点,且与直线l
3:5x-2y+3=0的夹角为
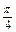
,求直线l的方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
两条曲线
y=
a|
x|和
y=
x+
a(
a>0)有两个不同的公共点,则
a的取值范围是
| A.a>1 | B.0<a<1 |
C.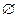 | D.0<a<1或a>1 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
.已知一曲线是与两个定点
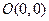
、

距离的比为
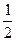
的点的轨迹,则求此曲线的方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
一条光线从点
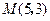
射出,被直线
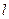
:
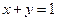
反射,入射光线到直线
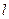
的角为
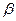
,已知
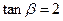
,求入射光线与反射光线所在的直线方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求纵截距为
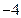
,且与两坐标轴围成三角形的面积为
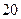
的直线的一般式方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图, 已知线段
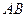
在直线
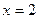
上移动,
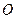
为原点.
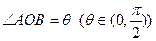
, 动点
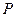
满足
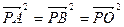
.
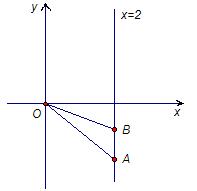
(Ⅰ) 求动点
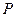
的轨迹方程;
(Ⅱ) 当
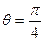
时, 动点
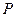
的轨迹与直线
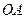
交于
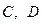
两点(点
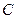
在点
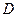
的下方), 且
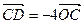
, 求直线
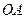
的方程.
查看答案和解析>>

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案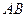 在直线
在直线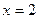 上移动,
上移动, 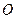 为原点.
为原点. 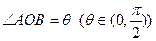 , 动点
, 动点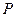 满足
满足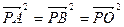 .
.
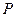 的轨迹方程;
的轨迹方程;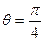 时, 动点
时, 动点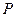 的轨迹与直线
的轨迹与直线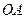 交于
交于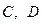 两点(点
两点(点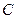 在点
在点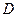 的下方), 且
的下方), 且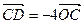 , 求直线
, 求直线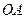 的方程.
的方程.