
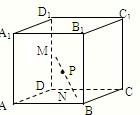
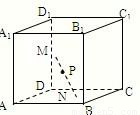
 已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动.则MN中点P的轨迹与该直平行六面体表面所围成的几何体中较小体积值为( )
已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动.则MN中点P的轨迹与该直平行六面体表面所围成的几何体中较小体积值为( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2π |
| 9 |


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
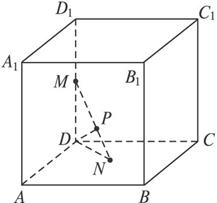
 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为| 2π |
| 9 |
| 2π |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二10月月考理科数学试卷(解析版) 题型:填空题
如右图已知每条棱长都为3的四棱柱ABCD-A B
B C
C D
D 中,底面是菱形,
中,底面是菱形, BAD=60°,D B
BAD=60°,D B ⊥平面ABCD,长为2的线段MN的一个端点M在DD
⊥平面ABCD,长为2的线段MN的一个端点M在DD 上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与此四棱柱的面所围成的几何体的体积为
_____________
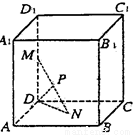
上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与此四棱柱的面所围成的几何体的体积为
_____________
查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市怀柔区高二(上)期末数学试卷(选修2-1)(理科)(解析版) 题型:选择题
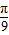
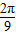
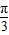
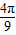
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com