
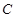 的方程为
的方程为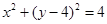 ,点
,点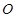 是坐标原点.直线
是坐标原点.直线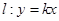 与圆
与圆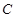 交于
交于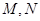 两点.
两点.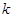 的取值范围;
的取值范围;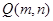 是线段
是线段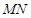 上的点,且
上的点,且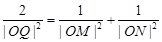 .请将
.请将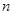 表示为
表示为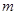 的函数.
的函数.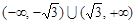 ; (2)
; (2)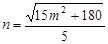 (
(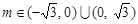 ).
).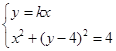 消去
消去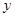 ,可得关于
,可得关于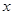 的一元二次方程
的一元二次方程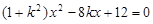 ,通过
,通过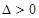 可得方程有两解,即直线和圆有两个交点; (2)由题中条件
可得方程有两解,即直线和圆有两个交点; (2)由题中条件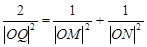 ,即先要求出
,即先要求出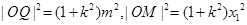 ,
,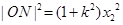 进而得出
进而得出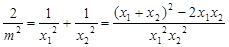 ,结合(1)中所求的一元二次方程运用韦达定理即可求出
,结合(1)中所求的一元二次方程运用韦达定理即可求出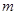 与
与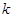 的关系式
的关系式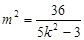 ,最后由点
,最后由点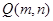 在直线
在直线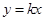 上,即可将
上,即可将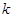 转化为
转化为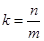 ,这样即可得出
,这样即可得出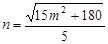 ,注意要由(1)中所求
,注意要由(1)中所求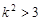 ,得到
,得到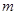 的范围.
的范围.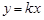 代入
代入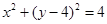 得 则
得 则 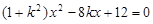 ,(*) 由
,(*) 由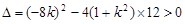 得
得 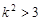 . 所以
. 所以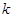 的取值范围是
的取值范围是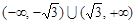
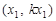 ,
,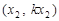 ,则
,则 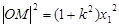 ,
,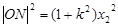 ,又
,又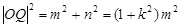 ,
, 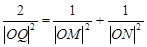 得,
得,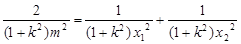 ,
, 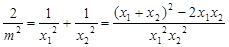
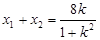 ,
,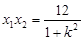 , 所以
, 所以 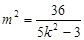 ,
, 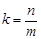 ,代入
,代入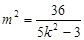 可得
可得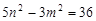 ,
, 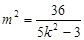 及
及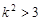 得
得 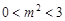 ,即
,即 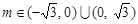 .
. 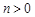 ,所以
,所以 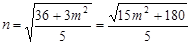 ,
, 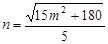 (
(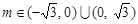 )
) 

 特高级教师点拨系列答案
特高级教师点拨系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com