
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
【答案】D
【解析】
根据函数的单调性可得an+1﹣an>0对于n∈N*恒成立,建立关系式,解之即可求出k的取值范围.
∵数列{an}中![]() ,且{an}单调递增
,且{an}单调递增
∴an+1﹣an>0对于n∈N*恒成立即(n+1)2﹣k(n+1)﹣(n2﹣kn)=2n+1﹣k>0对于n∈N*恒成立
∴k<2n+1对于n∈N*恒成立,即k<3
故选:D.
【点睛】
本题主要考查了数列的性质,本题易错误地求导或把它当成二次函数来求解,注意n的取值是解题的关键,属于易错题.
【题型】单选题
【结束】
8
【题目】已知等差数列{an}的前n项和为Sn,S4=40,Sn=210,Sn-4=130,则n=( )
A.12 B.14 C.16 D.18
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产的甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克) 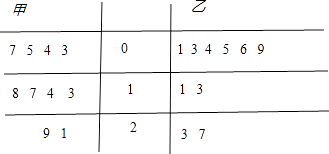
规定:当食品中的有害微量元素含量在[0,10]时为一等品,在(10,20]为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个.求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元.根据上表统计得到的甲、乙两种食品为一等品、二等品、劣质品,的频率分别估计这两种食品为,一等品、二等品、劣质品的概率.若分别从甲、乙食品中各抽取l件,设这两件食品给该厂带来的盈利为X,求随机变量X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( ) 
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 则一定有( )
则一定有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】本题主要考查不等关系。已知![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 。故选
。故选![]()
【题型】单选题
【结束】
5
【题目】关于x的不等式ax2+bx+2>0的解集为{x|-1<x<2},则关于x的不等式bx2-ax-2>0的解集为( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若lg(3x)+lg y=lg(x+y+1),则xy的最小值为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
先根据对称的运算性质化简得到3xy=x+y+1,再根据基本不等式即可求出答案.
∵lg(3x)+lgy=lg(3xy)=lg(x+y+1),x>0,y>0,
∴3xy=x+y+1,
∴3xy≥3![]() ,当且仅当x=y=1时取等号,
,当且仅当x=y=1时取等号,
即xy≥1,
∴xy的最小值是1,
故选:A
【点睛】
在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误
【题型】单选题
【结束】
12
【题目】已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设B、C是定点,且均不在平面α上,动点A在平面α上,且sin∠ABC=![]() , 则点A的轨迹为( )
, 则点A的轨迹为( )
A.圆或椭圆
B.抛物线或双曲线
C.椭圆或双曲线
D.以上均有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an+1.
(1)求数列{an}的通项公式;
(2)令bn=![]() n(an+1),求数列{bn}的前n项和Tn .
n(an+1),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线![]() 的方程;
的方程;
(2)过![]() 点的直线与曲线
点的直线与曲线![]() 交于
交于![]() 两点,
两点,![]() 点为坐标原点,求
点为坐标原点,求![]() 重心
重心![]() 的轨迹方程;
的轨迹方程;
(3)点![]() 是抛物线
是抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别是
的切线,切点分别是![]() .当
.当![]() 点在何处时,
点在何处时,![]() 的值最小?求出
的值最小?求出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com