练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】正四面体ABCD的棱长为2，棱AD与平面α所成的角θ∈[ ， ]，且顶点A在平面α内，B，C，D均在平面α外，则棱BC的中点E到平面α的距离的取值范围是（ ）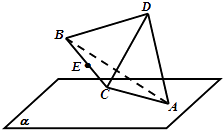

    A.[ ，1]
    B.[ ，1]
    C.[ ， ]
    D.[ ， ]

    【答案】C
    【解析】解：取平面DEA⊥平面α位置考虑即可．如图所示，
    在△ADE中，AD=2，DE=AE= ，
    ∴cos∠DAE= = ，
    棱AD与平面α所成的角为 时，sin∠EAN=sin（ ﹣∠DAE）
    = = ，
    ∴EN= （ ）=
    或sin∠EAN=sin（ +∠DAE）=
    ∴EN= （ ）=
    ∴棱BC的中点E到平面α的距离的取值范围是[ ， ]．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4－4：坐标系与参数方程

    在极坐标系中，曲线的极坐标方程是，以极点为原点，极轴为轴正半轴（两坐标系取相同的单位长度）的直角坐标系中，曲线的参数方程为：（为参数）．

    （1）求曲线的直角坐标方程与曲线的普通方程；

    （2）将曲线经过伸缩变换后得到曲线，若分别是曲线和曲线上的动点，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】天气预报说，在今后的三天中，每一天下雨的概率均为50%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用0，1，2，3，4表示下雨，用5，6，7，8，9表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：

    907 966 191 925 271 932 812 458 569 683

    431 257 393 027 556 488 730 113 537 989

    据此估计，这三天中恰有两天下雨的概率近似为（　　）

    A. 0.30 B. 0.35 C. 0.40 D. 0.50

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中， ，数列满足.

    （1）求证:数列是等差数列，写出的通项公式；

    （2）求数列的通项公式及数列中的最大项与最小项.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知M（﹣2，﹣3），N（3，0），直线l过点（﹣1，2）且与线段MN相交，则直线l的斜率k的取值范围是（　　）
    A.或k≥5
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数与（其中）在上的单调性正好相反，回答下列问题：

    （1）对于，，不等式恒成立，求实数的取值范围；

    （2）令，两正实数、满足，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的首项， ， …．

    （1）证明：数列是等比数列；

    （2）数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：

    （Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；

    （Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；

    （Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形面积之比为，第二小组频数为.

    （1）学生跳绳次数的中位数落在哪个小组内？

    （2）第二小组的频率是多少？样本容量是多少？

    （3）若次数在以上（含次）为良好，试估计该学校全体高一学生的良好率是多少？

    查看答案和解析>>

    同步练习册答案