已知函数f(x)=-x2+ax+lnx+b.
(Ⅰ)若函数f(x)在x=1处的切线方程为y=2,求a、b的值;
(Ⅱ)若a=1,函数f(x)的图象能否总在直线y=b+1的下方?若能,请加以证明;若不能,请说明理由.
解:(Ⅰ)∵f(x)=-x
2+ax+lnx+b
∴
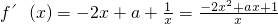
(2分)
∵函数f(x)在x=1处的切线方程为y=2,
∴
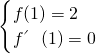
,即

,?
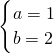
(4分)
(Ⅱ)当a=1时,f(x)=-x
2+x+lnx+b,定义域为(0,+∞)(5分)

(6分)
令f′(x)=0,得x=1或

(舍去)
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0
当x变化时,f′(x)、f(x)的变化情况如下表:

(8分)
∴f(x)在x=1处取极大值(9分)
又f(x)只有一个极大值,故它为最大值
∴f(x)
max=f(1)=b(10分)
∵f(1)=b<b+1,即f(x)
max<b+1
∴函数f(x)的图象总在直线y=b+1的下方(12分)
分析:(I)根据导数的几何意义求出函数f(x)在x=1处的导数,得到切线的斜率为0,以及切点在函数f(x)的图象上,建立方程组,解之即可求出a与b的值;
(II)先确定函数的定义域然后求导数fˊ(x),求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值,f(x)只有一个极大值,故它为最大值,欲使函数f(x)的图象总在直线y=b+1的下方,只需f(x)
max<b+1即可.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的极值等基础题知识,考查运算求解能力,属于基础题.

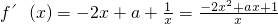 (2分)
(2分)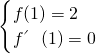 ,即
,即 ,?
,?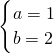 (4分)
(4分) (6分)
(6分) (舍去)
(舍去) (8分)
(8分)

 金钥匙试卷系列答案
金钥匙试卷系列答案