
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
| |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 | |
天数 | 6 | 14 | 18 | 27 | 25 | 20 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
(2)已知某企业每天因空气质量造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为![]() 元,求
元,求![]() 的分布列;
的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.
【答案】(1)![]() (2)(i)分布列见解析(ii)这3个月经济损失总额的数学期望会超过2.88万元,理由见详解.
(2)(i)分布列见解析(ii)这3个月经济损失总额的数学期望会超过2.88万元,理由见详解.
【解析】
(1)根据古典概型的概率计算公式即可容易求得;
(2)(i)求得![]() 的取值,再根据题意,求得对应取值的概率,则分布列得解;
的取值,再根据题意,求得对应取值的概率,则分布列得解;
(ii)根据(i)中所求,结合题意,求得![]() 个月因空气质量造成经济损失的总额,即可容易判断.
个月因空气质量造成经济损失的总额,即可容易判断.
(1)设![]() 为选取的3天中空气质量为优的天数,则
为选取的3天中空气质量为优的天数,则
![]() .
.
(2)(ⅰ)![]() 的可能取值为0,220,1480,
的可能取值为0,220,1480,
![]() ,
,
![]() ,
,
![]() ,
,
则![]() 的分布列为
的分布列为
| 0 | 220 | 1480 |
|
|
|
|
(ii)由(i)知![]() (元),
(元),
故该企业9月的经济损失的数学期望为![]() (元).
(元).
设该企业7月与8月每天因空气质量造成的经济损失为![]() 元,
元,
则![]() ,
,![]() ,
,
![]() ,
,
所以![]() (元),
(元),
所以7月与8月因空气质量造成经济损失的总额为![]() (元).
(元).
因为![]() 万,
万,
所以这3个月经济损失总额的数学期望会超过2.88万元.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥C﹣ABNM中,四边形ABNM的边长均为2,△ABC为正三角形,MB![]() ,MB⊥NC,E,F分别为MN,AC中点.
,MB⊥NC,E,F分别为MN,AC中点.
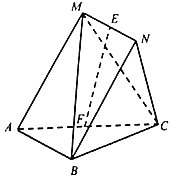
(Ⅰ)证明:MB⊥AC;
(Ⅱ)求直线EF与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有编号分别为1,2,3,4,5,6,7,8的八个小球和编号为1,2,3,4,5,6,7,8的八个盒子.现将这八个小球随机放入八个盒子内,要求每个盒子内放一个球,要求编号为偶数的小球在编号为偶数的盒子内,且至少有四个小球在相同编号的盒子内,则一共有______种投放方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k为常数,
(k为常数,![]() 且
且![]() ).
).
(1)在下列条件中选择一个________使数列![]() 是等比数列,说明理由;
是等比数列,说明理由;
①数列![]() 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
②数列![]() 是首项为4,公差为2的等差数列;
是首项为4,公差为2的等差数列;
③数列![]() 是首项为2,公差为2的等差数列的前n项和构成的数列.
是首项为2,公差为2的等差数列的前n项和构成的数列.
(2)在(1)的条件下,当![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() =(
=(![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ),设
),设![]() .
.
(1)求函数![]() 在[0,π]上的单调减区间;
在[0,π]上的单调减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,若![]() ,
,![]() ,求sinB的值.
,求sinB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()

A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com