
����Ŀ��ij��ѧ��ѧ��ʦ�ֱ������ֲ�ͬ��ѧ��ʽ����ѧ��ѧƽ���ֺ������ʶ���ͬ�ļס���������һ�°ࣨ������Ϊ![]() �ˣ����н�ѧ�������ѧ��ѧϰ��ѧ�ڷ̶ܳȺ��Ծ���һ�£�����ѧ���տ��Գɼ���Ҷͼ���£�
�ˣ����н�ѧ�������ѧ��ѧϰ��ѧ�ڷ̶ܳȺ��Ծ���һ�£�����ѧ���տ��Գɼ���Ҷͼ���£�
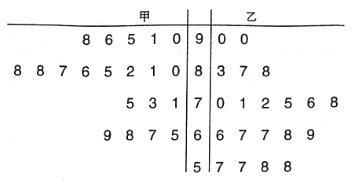
��1���ִ��Ұ���ѧ�ɼ�������![]() �ֵ�ͬѧ�������ȡ����ͬѧ����������һ���ɼ�Ϊ
�ֵ�ͬѧ�������ȡ����ͬѧ����������һ���ɼ�Ϊ![]() �ֵ�ͬѧ�����еĸ��ʣ�
�ֵ�ͬѧ�����еĸ��ʣ�
��2��ѧУ�涨���ɼ�������![]() �ֵ����㣬����д�����
�ֵ����㣬����д�����![]() ���������ж��ж�������Ϊ���ɼ��������ѧ��ʽ�йء���
���������ж��ж�������Ϊ���ɼ��������ѧ��ʽ�йء���
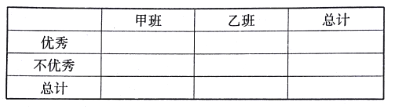
�����ο���ʽ������

���𰸡�(1) ![]() ;(2)�������.
;(2)�������.
�����������������(1) �Ұ���ѧ�ɼ�������![]() �ֵ�ͬѧ����
�ֵ�ͬѧ����![]() ��, ���������ȡ����ͬѧ����
��, ���������ȡ����ͬѧ����![]() ��,��û��һ���ɼ�Ϊ
��,��û��һ���ɼ�Ϊ![]() �ֵ�ͬѧ�����е��¼���Ϊ
�ֵ�ͬѧ�����е��¼���Ϊ![]() ��,���������һ���ɼ�Ϊ
��,���������һ���ɼ�Ϊ![]() �ֵ�ͬѧ�����е��¼���Ϊ
�ֵ�ͬѧ�����е��¼���Ϊ![]() ��,�����ݹŵ���������������Ϊ
��,�����ݹŵ���������������Ϊ![]() . (2)�����ݶ�Ӧ�������ʽ,�ɵ�
. (2)�����ݶ�Ӧ�������ʽ,�ɵ�![]() ,�ٶ�Ӧ�ο���ʽ�ɵð�����.
,�ٶ�Ӧ�ο���ʽ�ɵð�����.
�����������I���Ұ���ѧ�ɼ�������![]() �ֵ�ͬѧ����
�ֵ�ͬѧ����![]() ��,���гɼ�Ϊ
��,���гɼ�Ϊ![]() �ֵ�ͬѧ������,����״ͼ(��)֪,���������ȡ����ͬѧ����
�ֵ�ͬѧ������,����״ͼ(��)֪,���������ȡ����ͬѧ����![]() ��,������һ���ɼ�Ϊ
��,������һ���ɼ�Ϊ![]() �ֵ�ͬѧ�����е��¼���Ϊ
�ֵ�ͬѧ�����е��¼���Ϊ![]() ��,�������Ϊ
��,�������Ϊ![]() .
.
(��)��ͼ��ʾ
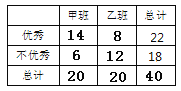
��![]() ֪, �����жϣ���
֪, �����жϣ���![]() ������Ϊ���ɼ��������ѧ��ʽ�йء�.
������Ϊ���ɼ��������ѧ��ʽ�йء�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ��лȫ��Ա���������Ͷ������������մ�л���ϣ�ͨ������ʽ��ȫ��˾1000λԱ�������ֽ�齱���涨��ÿλԱ����װ��4����ͬ�ʵ���Ĵ�����һ�����������2������4�����Ϸֱ��������![]() ��
��![]() ��
��![]() ��
��![]() �����������������ϵ�����֮��Ϊ��Ա������Ľ�����
�����������������ϵ�����֮��Ϊ��Ա������Ľ�����![]() ����λ��Ԫ������˾�ⶨ�������������ַ�����
����λ��Ԫ������˾�ⶨ�������������ַ�����
���� |
|
|
|
|
һ | 100 | 100 | 100 | 500 |
�� | 100 | 100 | 500 | 500 |
�� | 200 | 200 | 400 | 400 |
���������ȡ����һ����![]() �ĸ��ʣ�
�ĸ��ʣ�
���ֱ���㷽��������������ƽ����![]() �ͷ���
�ͷ���![]() �����Ҫ��Ա������Ľ�������Ծ��⣬�������ͷ�����ѡ���ĸ����ã�
�����Ҫ��Ա������Ľ�������Ծ��⣬�������ͷ�����ѡ���ĸ����ã�
������ͶƱѡ�������Ƿ�����ʱ����˾���Ա�ֲ��ȡ100��Ա������ͳ�ƣ��õ����²�������![]() ���������뽫�ñ��������������ж��ܷ���90%�İ�����Ϊ��ѡ�����������Ա��йء���
���������뽫�ñ��������������ж��ܷ���90%�İ�����Ϊ��ѡ�����������Ա��йء���
������ | ������ | �ϼ� | |
���� | 12 | ||
�� | 40 | ||
�ϼ� | 82 | 100 |
����![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|2x+![]() |+a|x��
|+a|x��![]() |��
|��
��������a=��1ʱ���ⲻ��ʽf��x����3x��
��������a=2ʱ��������x�IJ���ʽ2f��x��+1��|1��b|�Ľ⼯Ϊ�ռ�����ʵ��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�����ABB1A1�͵���ABC��CA=CB��D��E��F�ֱ�ΪAB��A1D��A1C���е㣬��G��AA1�ϣ���A1D��EG�� 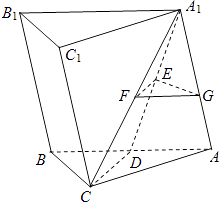
��1����֤��CD��ƽ��EFG��
��2����֤��A1D��ƽ��EFG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲM��Բ��ΪM����1��2����ֱ��y=x+4��ԲM�صõ��ҳ�Ϊ ![]() ����P��ֱ��l��y=x��1�ϣ�
����P��ֱ��l��y=x��1�ϣ�
��1����ԲM�ı����̣�
��2�����Q��ԲM�ϣ������� ![]() =4
=4 ![]() �����P�����ꣻ
�����P�����ꣻ
��3����뾶Ϊ5��ԲN��ԲM���룬����P�ֱ���ԲM��ԲN�����ߣ��е�ֱ�ΪA��B����������ĵ�P������PA=PB��������Բ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijý��Ϊ�˽�ij������ѧ�����Ϸ�ѧ��ʹ���ֻ���������������ȡ��100����ѧ�����е��飮��ͼ�Ǹ��ݵ��������Ƶ�ѧ��ÿ��ʹ���ֻ�����ƽ������ʱ���Ƶ�ʷֲ�ֱ��ͼ����ʱ�䲻����40���ӵ�ѧ����Ϊ���ֻ��ԡ��� 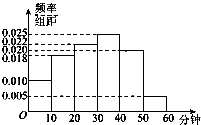
��1�������С��ֻ��ԡ��ж����ˣ�
��2��������֪������������2��2�����������ݴ������ж��Ƿ���95%�İ�����Ϊ���ֻ��ԡ����Ա��йأ�
��3���������������õ���Ƶ����Ϊ���ʣ����ڴӸõ���������ѧ ���У����������������ÿ�γ�ȡ1����ѧ������ȡ3�Σ�������һ�����ֻ��ԡ��ȡ����ֻ��ԡ�ÿ�µĻ���ƽ����40Ԫ���DZ���ȡ��3����ѧ���еġ��ֻ��ԡ�����ΪX������3��ÿ�µ��ܻ��ѱȡ����ֻ��ԡ������YԪ����ÿ�γ�ȡ�Ľ����������ģ���X�ķֲ��к�Y������EY
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2����Ʒ��3����Ʒ�����һ������Ҫͨ����⽫�����֣�ÿ�����һ����Ʒ�����Żأ�ֱ������2����Ʒ������3����Ʒʱ��������
��1�����һ�μ������Ǵ�Ʒ�ҵڶ��μ���������Ʒ�ĸ��ʣ�
��2����֪ÿ���һ����Ʒ��Ҫ����100Ԫ����X��ʾֱ������2����Ʒ������3����Ʒʱ����Ҫ�ļ����ã���λ��Ԫ������X�ķֲ��к;�ֵ����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����an+1+an=4n��3��n��N*
��1��������{an}�ǵȲ����У���a1��ֵ��
��2����a1=��3ʱ��������{an}��ǰn���Sn��
��3�����������n��N* �� ���� ![]() ��5��������a1��ȡֵ��Χ��
��5��������a1��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ϵ�ļ���Ϊֱ������ϵ��ԭ�㣬����Ϊx��������ᣬ��������ϵ�еij��ȵ�λ��ͬ����֪����C�ļ����귽��Ϊ��=2��cos��+sin�ȣ���
��1����C��ֱ�����귽�̣�
��2��ֱ��l�� 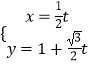 Ϊ������������C����A��B���㣬��y�ύ��E����|EA|+|EB|��ֵ��
Ϊ������������C����A��B���㣬��y�ύ��E����|EA|+|EB|��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com