[题目]已知0＜x＜1.0＜y＜1. 求证 + + + ≥2 .并求使等号成立的条件．题目和参考答案——青夏教育精英家教网—

【题目】已知0＜x＜1，0＜y＜1，求证 + + + ≥2 ，并求使等号成立的条件．

【答案】证明：∵0＜x＜1，0＜y＜1，设P（x，y），A（1，0），B（1，1），C（0，1），如图：则|PO|= ，|PA|= ，|PB|= ，|PC|= ，
∵|PO|+|PB|≥|BO|= ，|PA|+|PC|≥|AC|=
∴|PO|+|PB|+|PA|+|PC|≥2 （当且仅当点P为正方形的对角线AC与OB的交点是取等号），
即x=y= 时取等号．
∴ + + + ．

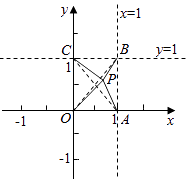
【解析】依题意，作图如下，利用两点间的距离公式可知|PO|= ，|PA|= ，|PB|= ，|PC|= ，利用三角不等式可证|PO|+|PB|+|PA|+|PC|≥2
【考点精析】解答此题的关键在于理解二维形式的柯西不等式的相关知识，掌握二维形式的柯西不等式：当且仅当时，等号成立．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】据调查，某地区有300万从事传统农业的农民，人均年收入6000元，为了增加农民的收入，当地政府积极引进资本，建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作，据估计，如果有万人进企业工作，那么剩下从事传统农业的农民的人均年收入有望提高，而进入企业工作的农民的人均年收入为元．

（1）在建立加工企业后，多少农民进入企业工作，能够使剩下从事传统农业农民的总收入最大，并求出最大值；

（2）为了保证传统农业的顺利进行，限制农民加入加工企业的人数不能超过总人数的，当地政府如何引导农民，即取何值时，能使300万农民的年总收入最大．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在下列命题中，①的一个充要条件是与它的共轭复数相等：

②利用独立性检验来考查两个分类变量，是否有关系，当随机变量的观测值值越大，“与有关系”成立的可能性越大；

③在回归分析模型中，若相关指数越大，则残差平方和越小，模型的拟合效果越好；

④若，是两个相等的实数，则是纯虚数；

⑤某校高三共有个班，班有人，班有人，班有人，由此推测各班都超过人，这个推理过程是演绎推理.

其中真命题的序号为__________．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】f（n）=1+ + +…+ （n∈N*），计算可得f（2）= ，f（4）＞2，f（8）＞，f（16）＞3，f（32）＞，推测当n≥2时，有．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在中,已知，在上，且，又平面.

（Ⅰ）求证：平面；

（Ⅱ）求二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图是函数y=Asin（ωx+φ）（A＜0，ω＞0，|φ|≤ ）图象的一部分．为了得到这个函数的图象，只要将y=sinx（x∈R）的图象上所有的点（）
A.向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变
B.向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变
C.向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变
D.向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变