
分析 (1)求得函数的定义域,求导函数,确定函数的单调性,即可求得函数f(x)的最小值.
(2)分类讨论,利用导数的正负,即可得到函数F(x)的单调性.
解答 解:函数的定义域为(0,+∞)
求导函数,可得f′(x)=1+lnx,
令f′(x)=1+lnx=0,可得x=$\frac{1}{e}$,
∴0<x<$\frac{1}{e}$时,f′(x)<0,x>$\frac{1}{e}$时,f′(x)>0,
∴x=$\frac{1}{e}$时,函数取得极小值,也是函数的最小值,
∴f(x)min=f($\frac{1}{e}$)=$\frac{1}{e}$•ln$\frac{1}{e}$=-$\frac{1}{e}$;
(2)F(x)=ax2+lnx+1(x>0),F′(x)=$\frac{2{ax}^{2}+1}{x}$(x>0).
①当a≥0时,恒有F′(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,令F′(x)>0,得2ax2+1>0,解得0<x<$\sqrt{-\frac{1}{2a}}$;
令F′(x)<0,得2ax2+1<0,解得x>$\sqrt{-\frac{1}{2a}}$.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在(0,$\sqrt{-\frac{1}{2a}}$)上单调递增,在($\sqrt{-\frac{1}{2a}}$,+∞)上单调递减.
点评 本题考查导数知识的运用,考查函数的最值,考查学生分析解决问题的能力,属于中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
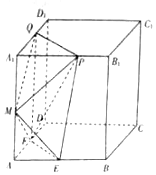 如图,正方体ABCD-A1B1C1D1中,E、F,M分别是AB,AM,AA1的中点,P,Q分别是A1B1,A1D1上的动点(不与A1重合),且A1P=A1Q.
如图,正方体ABCD-A1B1C1D1中,E、F,M分别是AB,AM,AA1的中点,P,Q分别是A1B1,A1D1上的动点(不与A1重合),且A1P=A1Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PD⊥AB,平面PAB⊥平面ABCD,点E,F为棱PB,PC中点,二面角F-AD-C的平面角的余弦值为$\frac{3\sqrt{13}}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com