练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，已知曲线与曲线，（为参数）．以坐标原点为极点，轴的正半轴为极轴建立极坐标系．

    （1）写出曲线，的极坐标方程；

    （2）在极坐标系中，已知与，的公共点分别为，，，当时，求的值．

    【答案】（1）的极坐标方程为：；的极坐标方程为： （2）

    【解析】

    （1）根据直角坐标与极坐标的互化关系，参数方程与一般方程的互化关系，即得解；

    （2）将代入，的极坐标方程，求得的表达式，代入，即得解.

    （1）解：将直角坐标与极坐标互化关系代入曲线

    得，

    即：；

    所以曲线的极坐标方程为：；

    又曲线（为参数）．

    利用消去参数得，

    将直角坐标与极坐标互化关系：

    代入上式化简得，

    所以曲线的极坐标方程为：．

    （2）∵与曲线，的公共点分别为，，

    所以将代入及

    得，，

    又，∴，

    ∴，∴，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数()，().

    （1）若恒成立，求实数的取值范围；

    （2）当时，过上一点作的切线，判断：可以作出多少条切线，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在单调递增，求的范围；

    （2）讨论的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆柱OO1底面半径为1，高为π，ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D，其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ（0＜θ＜π）后，边B1C1与曲线Γ相交于点P.

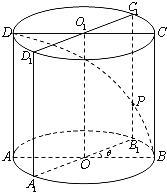
    （1）求曲线Γ长度；

    （2）当时，求点C1到平面APB的距离；

    （3）是否存在θ，使得二面角D﹣AB﹣P的大小为？若存在，求出线段BP的长度；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由于《中国诗词大会》节目在社会上反响良好，某地也模仿并举办民间诗词大会，进入正赛的条件为：电脑随机抽取10首古诗，参赛者能够正确背诵6首及以上的进入正赛．若诗词爱好者甲、乙参赛，他们背诵每一首古诗正确的概率均为．

    （1）求甲进入正赛的概率．

    （2）若参赛者甲、乙都进入了正赛，现有两种赛制可供甲、乙进行PK，淘汰其中一人．

    赛制一：积分淘汰制，电脑随机抽取4首古诗，每首古诗背诵正确加2分，错误减1分．由于难度增加，甲背诵每首古诗正确的概率为，乙背诵每首古诗正确的概率为，设甲的得分为，乙的得分为．

    赛制二：对诗淘汰制，甲、乙轮流互出诗名，由对方背诵且互不影响，乙出题，甲回答正确的概率为0.3，甲出题，乙回答正确的概率为0.4，谁先背诵错误谁先出局．

    （i）赛制一中，求甲、乙得分的均值，并预测谁会被淘汰；

    （ii）赛制二中，谁先出题甲获胜的概率大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数，），曲线的参数方程为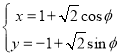（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系.

    （1）求曲线的极坐标方程；

    （2）设曲线与曲线的交点分别为，求的最大值及此时直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春节期间，全国人民都在抗击“新型冠状病毒肺炎”的斗争中.当时武汉多家医院的医用防护物资库存不足，某医院甚至面临断货危机，南昌某生产商现有一批库存的医用防护物资，得知消息后，立即决定无偿捐赠这批医用防护物资，需要用A、B两辆汽车把物资从南昌紧急运至武汉.已知从南昌到武汉有两条合适路线选择，且选择两条路线所用的时间互不影响.据调查统计2000辆汽车，通过这两条路线从南昌到武汉所用时间的频数分布表如下：

    所用的时间（单位：小时）

    路线1的频数

    200

    400

    200

    200

    路线2的频数

    100

    400

    400

    100

    假设汽车A只能在约定交货时间的前5小时出发，汽车B只能在约定交货时间的前6小时出发（将频率视为概率）.为最大可能在约定时间送达这批物资，来确定这两车的路线.

    （1）汽车A和汽车B应如何选择各自的路线.

    （2）若路线1、路线2的“一次性费用”分别为3.2万元、1.6万元，且每车医用物资生产成本为40万元（其他费用忽略不计），以上费用均由生产商承担，作为援助金额的一部分.根据这两辆车到达时间分别计分，具体规则如下（已知两辆车到达时间相互独立，互不影响）：

    到达时间与约定时间的差x（单位：小时）

    该车得分

    0

    1

    2

    生产商准备根据运输车得分情况给出现金排款，两车得分和为0，捐款40万元，两车得分和每增加1分，捐款增加20万元，若汽车A、B用（1）中所选的路线运输物资，记该生产商在此次援助活动中援助总额为Y（万元），求随机变量Y的期望值，（援助总额一次性费用生产成本现金捐款总额）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，图中直棱柱的底面是菱形，其中.又点分别在棱上运动，且满足：，.

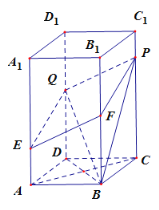
    （1）求证：四点共面，并证明∥平面.

    （2）是否存在点使得二面角的余弦值为？如果存在，求出的长；如果不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线和圆，倾斜角为45°的直线过抛物线的焦点，且与圆相切．

    （1）求的值；

    （2）动点在抛物线的准线上，动点在上，若在点处的切线交轴于点，设．求证点在定直线上，并求该定直线的方程．

    查看答案和解析>>

    同步练习册答案