
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对于任意
,对于任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对于任意正整数
,求证:对于任意正整数![]() ,都有
,都有![]() ;
;
(3)将数列![]() 、
、![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面”,“当
放在前面”,“当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”得到一个新的数列:
放在前面”的要求进行“交叉排列”得到一个新的数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 求这个新数列的前
求这个新数列的前![]() 项和
项和![]() .
.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)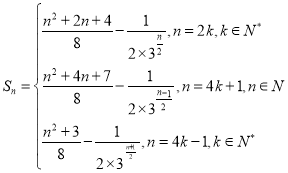 .
.
【解析】
(1)由题意可知数列![]() 为等差数列,确定该数列的首项和公差,可求出数列
为等差数列,确定该数列的首项和公差,可求出数列![]() 的通项公式,可求出
的通项公式,可求出![]() ,再由
,再由 可求出数列
可求出数列![]() 的通项公式,由等差中项法可知数列
的通项公式,由等差中项法可知数列![]() 为等差数列,从而可得出数列
为等差数列,从而可得出数列![]() 为等比数列,且设该等比数列的公比为
为等比数列,且设该等比数列的公比为![]() ,结合题中条件求出
,结合题中条件求出![]() 和
和![]() 的值,即可求出数列
的值,即可求出数列![]() 的通项公式;
的通项公式;
(2)利用错位相减法求出数列![]() 的前
的前![]() 项和
项和![]() ,即可证明出
,即可证明出![]() ;
;
(3)求出数列![]() 的前
的前![]() 项和
项和![]() ,对
,对![]() 进行分类讨论,利用等差数列和等比数列的求和公式可得出
进行分类讨论,利用等差数列和等比数列的求和公式可得出![]() .
.
(1)![]() 且
且![]() ,所以,数列
,所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列,
为公差的等差数列,![]() ,
,![]() .
.
当![]() 时,
时,![]() .
.
![]() 也适合上式,所以,
也适合上式,所以,![]() .
.
![]() ,即
,即![]() ,
,
所以,数列![]() 为等差数列,设其公差为
为等差数列,设其公差为![]() ,则
,则![]() ,
,
![]() ,所以,数列
,所以,数列![]() 是正项等比数列,设其公比为
是正项等比数列,设其公比为![]() ,则
,则![]() .
.
由题意可得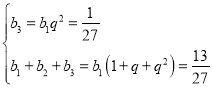 ,解得
,解得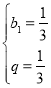 ,
,
因此,![]() ;
;
(2)![]() ,
,
![]() ,①
,①
则![]() ,②
,②
①![]() ②得
②得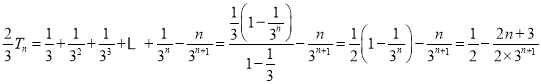 ,
,
化简得![]() ;
;
(3)数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为 ,
,
①当![]() 时,
时,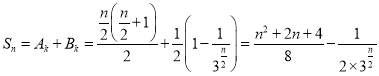 ;
;
②当![]() 时,
时,![]()
 ,
,
特别地,当![]() 时,
时,![]() 也适合上式;
也适合上式;
③当![]() 时,
时,![]()
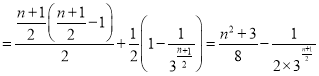 .
.
综上所述,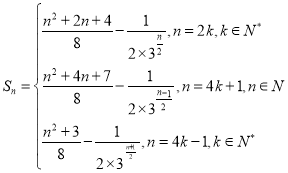 .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 、
、![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项大于0的等差数列![]() 的公差
的公差![]() ,且
,且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;
;
①求数列![]() 的通项
的通项![]() ;
;
②是否存在实数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为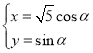 (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 与曲线
与曲线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (且点
(且点![]() ,
,![]() 均异于原点
均异于原点![]() ),当
),当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
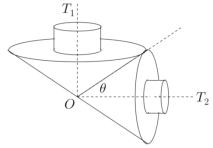
【题目】如图所示,某传动装置由两个陀螺![]() ,
,![]() 组成,陀螺之间没有滑动,每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的
组成,陀螺之间没有滑动,每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的![]() ,且
,且![]() ,
,![]() 的轴相互垂直,它们相接触的直线与
的轴相互垂直,它们相接触的直线与![]() 的轴所成角
的轴所成角![]() ,若陀螺
,若陀螺![]() 中圆锥的底面半径为
中圆锥的底面半径为![]() (
(![]() );
);
(1)求陀螺![]() 的体积;
的体积;
(2)当陀螺![]() 转动一圈时,陀螺
转动一圈时,陀螺![]() 中圆锥底面圆周上一点
中圆锥底面圆周上一点![]() 转动到点
转动到点![]() ,求
,求![]() 与
与![]() 之间的距离;
之间的距离;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若
,若![]() (
(![]() 是与
是与![]() 无关的常数,
无关的常数,![]() )则称数列
)则称数列![]() 叫做“弱等差数列”已知数列
叫做“弱等差数列”已知数列![]() 满足:
满足:![]() 且
且![]() ,对于
,对于![]() 恒成立,(其中
恒成立,(其中![]() 都是常数)
都是常数)
(1)求证:数列![]() 是“弱等差数列”,并求出数列
是“弱等差数列”,并求出数列![]() 的通项公式
的通项公式
(2)当![]() 时,若数列
时,若数列![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围
的取值范围
(3)若![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为___________.
②抽取的总人数的最小值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com