
【题目】已知等差数列![]() 的公差不为零,且
的公差不为零,且![]() ,
,![]() 、
、![]() 、
、![]() 成等比数列,数列
成等比数列,数列![]() 满足
满足![]()
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)求证: .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,运用等差数列的通项公式和等比数列的中项性质,解方程可得首项和公差,进而得到
,运用等差数列的通项公式和等比数列的中项性质,解方程可得首项和公差,进而得到![]() ,可令
,可令![]() ,求得
,求得![]() ,再将
,再将![]() 换为
换为![]() ,相减可得
,相减可得![]() ;
;
(2)原不等式转化为![]() ,应用数学归纳法证明,注意检验
,应用数学归纳法证明,注意检验![]() 时不等式成立,再假设
时不等式成立,再假设![]() 时不等式成立,证明
时不等式成立,证明![]() 时,不等式也成立,注意运用分析法证明.
时,不等式也成立,注意运用分析法证明.
(1)等差数列![]() 的公差
的公差![]() 不为零,
不为零,![]() ,可得
,可得![]() ,
,
![]() 、
、![]() 、
、![]() 成等比数列,可得
成等比数列,可得![]() ,即
,即![]() ,
,
解方程可得![]() ,则
,则![]() .
.
数列![]() 满足
满足![]() ,可得
,可得![]() ,
,
当![]() 时,由
时,由![]() ,
,
可得![]() ,
,
相减可得![]() ,则
,则![]() ,
,![]() 也适合
也适合![]() ,则
,则![]() ,
,![]() ;
;
(2)证明:不等式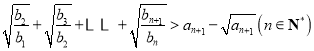 即为
即为
![]() ,
,
下面应用数学归纳法证明.
(i)当![]() 时,不等式的左边为
时,不等式的左边为![]() ,右边为
,右边为![]() ,左边
,左边![]() 右边,不等式成立;
右边,不等式成立;
(ii)假设![]() 时,不等式
时,不等式![]() 成立,
成立,
当![]() 时,
时,![]() ,
,
要证![]() ,
,
只要证![]() ,
,
即证![]() ,
,
即证![]() ,
,
由![]() ,可得上式成立,可得
,可得上式成立,可得![]() 时,不等式也成立.
时,不等式也成立.
综上可得,对一切![]() ,
,![]() ,
,
故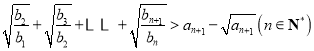 .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】设离心率为3,实轴长为1的双曲线![]() (
(![]() )的左焦点为
)的左焦点为![]() ,顶点在原点的抛物线
,顶点在原点的抛物线![]() 的准线经过点
的准线经过点![]() ,且抛物线
,且抛物线![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,且满足
,且满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2019年的高考考生人数是2016年高考考生人数的1.2倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考情况,得到如图柱状图:

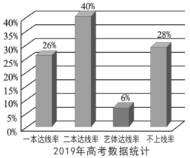
则下列结论正确的是( ).
A.与2016年相比,2019年不上线的人数有所增加
B.与2016年相比,2019年一本达线人数减少
C.与2016年相比,2019年二本达线人数增加了0.3倍
D.2016年与2019年艺体达线人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )

A.2017年第一季度GDP增速由高到低排位第5的是浙江省
B.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
C.去年同期河南省的GDP总量不超过4000亿元
D.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为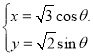 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com