
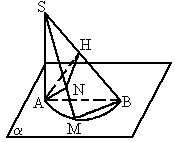
平面α内有一个半圆,直径为AB,过A作SA⊥平面α,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.
(1)求证:NH⊥SB.
(2)这个图形中有多少个线面垂直关系?
(3)这个图形中有多少个直角三角形?
(4)这个图形中有多少对相互垂直的直线?
|
解:(1)连AM,BM.∵AB为已知圆的直径,如图所示.
∴AM⊥BM, ∵SA⊥平面α,MB ∴SA⊥MB. ∵AM∩SA=A,∴BM⊥平面SAM. ∵AN ∴BM⊥AN. ∵AN⊥SM于N,BM∩SM=M, ∴AN⊥平面SMB. ∵AH⊥SB于H,且NH是AH在平面SMB的射影 ∴NH⊥SB. (2)由(1)知,SA⊥平面AMB,BM⊥平面SAM.AN⊥平面SMB. ∵SB⊥AH且SB⊥HN. ∴SB⊥平面ANH. ∴图中共有4个线面垂直关系 (3)∵SA⊥平面AMB, ∴ΔSAB、ΔSAM均为直角三角形. ∵BM⊥平面SAM,∴ΔBMA,ΔBMS均为直角三角形. ∵AN⊥平面SMB.∴ΔANS、ΔANM、ΔANH均为直角三角形. ∵SB⊥平面AHN.∴ΔSHA、ΔBHA、ΔSHN均为直角三角形 综上所述,图中共有10个直角三角形. (4)由SA⊥平面AMB知:SA⊥AM,SA⊥AB,SA⊥BM; 由BM⊥平面SAM知:BM⊥AM,BM⊥SM,BM⊥AN; 由AN⊥平面SMB知:AN⊥SM,AN⊥SB,AN⊥NH; SB⊥平面AHN知:SB⊥AH,SB⊥HN; 综上所述,图中有11对互相垂直的直线. 解析:此题主要考查直线与直线,直线与平面的垂直关系及论证,空间想象力. |


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
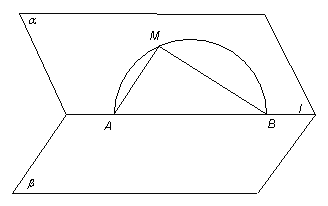
 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
如图,平面a内有一个半圆,直径为AB,过A作SA⊥平面a,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.这个图形中有多少对垂直的直线?
查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,平面
a内有一个半圆,直径为AB,过A作SA⊥平面a,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.这个图形中有多少对垂直的直线?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
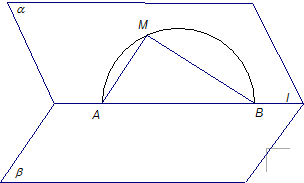 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.查看答案和解析>>
科目:高中数学 来源:2010年长春市十一高中高一下学期期末考试(数学理) 题型:解答题
如图,已知二面角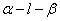 的平面角为
的平面角为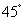 ,
在半平面
,
在半平面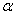 内有一个半圆
内有一个半圆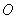 ,
其直径
,
其直径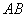 在
在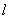 上,
上, 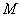 是这个半圆
是这个半圆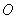 上任一点(除
上任一点(除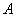 、
、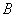 外), 直线
外), 直线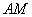 、
、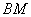 与另一个半平面
与另一个半平面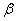 所成的角分别为
所成的角分别为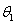 、
、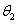 .试证明
.试证明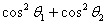 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com