
分析 (1)设它们的夹角为θ,利用向量的数量积公式表示出cosθ,将已知条件代入,利用特殊角的三角函数值求出两个向量的夹角.
(2)利用向量模的坐标公式将已知条件转化为λ2-2λsin(α-β)+1≥4对任意的α,β恒成立,再结合正弦函数的有界性,建立关于λ的不等式组,解之可得满足条件的实数λ的取值范围
解答 解:(1)设它们的夹角为θ,∵向量$\overrightarrow{OA}$=(λcosα,λsinα)(λ≠0),$\overrightarrow{OB}$=(-sinβ,cosβ),
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=-λcosαsinβ+λsinαcosβ=λsin(α-β)=λsin$\frac{π}{6}$=$\frac{λ}{2}$,
|$\overrightarrow{OA}$|=|λ|=-λ,|$\overrightarrow{OB}$|=1,
∴cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}||\overrightarrow{OB|}}$=$\frac{\frac{λ}{2}}{-λ×1}$=-$\frac{1}{2}$,
∴θ=$\frac{2π}{3}$,
(2)∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$,
∴|$\overrightarrow{AB}$|2=|$\overrightarrow{OB}$-$\overrightarrow{OA}$|2=|$\overrightarrow{OB}$|2+|$\overrightarrow{OA}$|2-2$\overrightarrow{OA}$•$\overrightarrow{OB}$=1+λ2-2λsin(α-β),
∵|$\overrightarrow{AB}$|≥2|$\overrightarrow{OB}$|对于任意实数α,β都成立,
∴λ2-2λsin(α-β)+1≥4,
即λ2-2λsin(α-β)-3≥0对任意实数α、β都成立
∵-1≤sin(α-β)≤1,
∴$\left\{\begin{array}{l}{{λ}^{2}-2λ-3≥0}\\{{λ}^{2}+2λ-3≥0}\end{array}\right.$
解得λ≤-3或λ≥3.
点评 本题综合了平面向量的数量积、和与差的三角函数以及不等式恒成立等知识点,属于难题.解题时应该注意等价转化和函数方程思想的运用.


科目:高中数学 来源: 题型:选择题
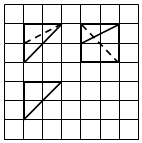 如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | 2 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 5 | C. | $\sqrt{31}$ | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
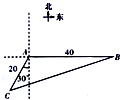 如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$.
如图,位于A处的海面观测站获悉,在其正东方向相距40海里的B处有一艘渔船遇险,并在原地等待营救.在A处南偏西30°且相距20海里的C处有一艘救援船,该船接到观测站通告后立即前往B处求助,则sin∠ACB=$\frac{\sqrt{21}}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 0 | D. | -2或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com