
对关于 的一元二次方程
的一元二次方程 ……
…… ,解决下列两个问题:
,解决下列两个问题:
(1)若 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,求方程
三个数中任取的一个数,求方程 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求方程
任取的一个数,求方程 有两个不相等实根的概率.
有两个不相等实根的概率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
A、B两个试验方案在某科学试验中成功的概率相同,已知A、B两个方案至少一个方案试验成功的概率是0.36.
(1)求两个方案均获成功的概率;
(2)设试验成功的方案的个数为随机变量ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从集合 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定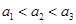
(1)从所有三元有序数组中任选一个,求它的所有元素之和等于10的概率;
(2)定义三元有序数组 的“项标距离”为
的“项标距离”为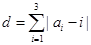 ,(其中
,(其中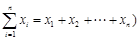 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”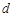 为偶数的概率;
为偶数的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为
40秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3) 不是红灯
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为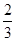 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为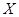 ,求
,求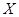 的分布列;
的分布列;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为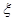 ;乙用这枚硬币掷2次,记正面朝上的次数为
;乙用这枚硬币掷2次,记正面朝上的次数为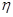 。
。
(1)分别求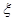 与
与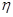 的期望;
的期望;
(2)规定:若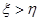 ,则甲获胜;若
,则甲获胜;若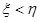 ,则乙获胜,分别求出甲和乙获胜的概率.
,则乙获胜,分别求出甲和乙获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为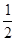 ,
,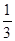 ,
,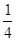 ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.
(1)求该参加者有资格闯第三关的概率;
(2)求ζ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
(2)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的一位顾客购买甲、乙两种商品中的一种的概率;
(2) 求进入商场的一位顾客至少购买甲、乙两种商品中的一种的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com