
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断并证明函数![]() 的单调性;
的单调性;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆C的左、右焦点坐标分别是![]() ,
,![]() ,离心率是
,离心率是![]() ,直线
,直线![]() 与椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P.
与椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的离心率为
的离心率为![]() ,且点
,且点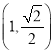 在此椭圆上.
在此椭圆上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() .两点.若
.两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
①已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() ;
;
②相关系数r用来衡量两个变量之间线性关系的强弱,![]() 越大,相关性越弱;
越大,相关性越弱;
③相关指数![]() 用来刻画回归的效果,
用来刻画回归的效果,![]() 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
④在残差图中,残差点分布的带状区域越狭窄,其模型拟合的精度就越高.
A.①②B.①④C.②③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD是菱形,AC与BD交于点O,![]() 底面ABCD,点M为PC中点,
底面ABCD,点M为PC中点,![]() ,
,![]() ,
,![]() .
.
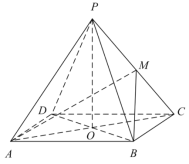
(1)求异面直线AP与BM所成角的余弦值;
(2)求平面ABM与平面PAC所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com