
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C截直线y=1所得线段的长度为2
,椭圆C截直线y=1所得线段的长度为2 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|.设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求∠EDF的最小值.
【答案】解:(Ⅰ)∵椭圆C的离心率为 ![]() ,
,
∴ ![]() =
= ![]() ,a2=2b2 ,
,a2=2b2 ,
∵椭圆C截直线y=1所得线段的长度为2 ![]() ,
,
∴椭圆C过点( ![]() ,1),
,1),
∴ ![]() +
+ ![]() =1,
=1,
∴b2=2,a2=4,
∴椭圆C的方程为 ![]() +
+ ![]() =1.
=1.
(Ⅱ)设A,B的横坐标为x1 , x2 ,
则A(x1 , kx1+m),B(x2 , kx2+m),D( ![]() ,
, ![]() +m),
+m),
联立  可得(1+2k2)x2+4kmx+2m2﹣4=0,
可得(1+2k2)x2+4kmx+2m2﹣4=0,
∴x1+x2=﹣ ![]() ,
,
∴D(﹣ ![]() ,
, ![]() ),
),
∵M(0,m),则N(0,﹣m),
∴⊙N的半径为|m|,
|DN|= ![]() =
= ![]() ,
,
设∠EDF=α,
∴sin ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
令y= ![]() ,则y′=
,则y′= ![]() ,
,
当k=0时,sin ![]() 取得最小值,最小值为
取得最小值,最小值为 ![]() .
.
∴∠EDF的最小值是60°.
【解析】(Ⅰ)首先根据题中信息可得椭圆C过点( ![]() ,1),然后结合离心率可得椭圆方程;(Ⅱ)可将题目所求角度的最小值转化为求角度正弦的最小值,结合题目信息可求得D、N坐标及⊙N半径,进而将DN长度表示出来,可求∠EDF最小值.
,1),然后结合离心率可得椭圆方程;(Ⅱ)可将题目所求角度的最小值转化为求角度正弦的最小值,结合题目信息可求得D、N坐标及⊙N半径,进而将DN长度表示出来,可求∠EDF最小值.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|3x﹣ ![]() |.
|.
(1)求不等式f(x)<1的解集;
(2)若实数a,b,c满足a>0,b>0,c>0且a+b+c= ![]() .求证:
.求证: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A-BCDE中,底面BCDE是等腰梯形,BC∥ DE,∠ DCB=45°,O是BC中点,AO=![]() ,且BC=6,AD=AE=2CD=
,且BC=6,AD=AE=2CD=![]() .
.
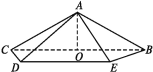
(1)证明:AO⊥平面BCD;
(2)求二面角A-CD-B的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1 , A2 , A3和3个欧洲国家B1 , B2 , B3中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2![]() ,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.
,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
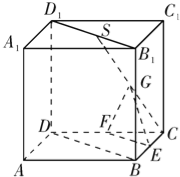
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com