
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).

(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所发现,一种作物的年收获量 ![]() (单位:
(单位: ![]() )与它“相近”作物的株数
)与它“相近”作物的株数 ![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 ![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为 ![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求该作物的年收获量 ![]() 关于它“相近”作物的株数
关于它“相近”作物的株数![]() 的线性回归方程;
的线性回归方程;
(2)农科所在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每
个小正方形的面积为 ![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收
获量以线性回归方程计算所得数据为依据)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估
计分别为, 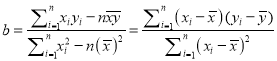 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
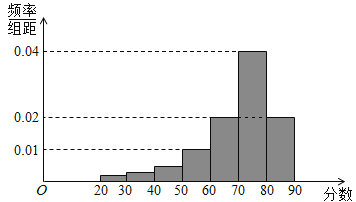
(1)若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(2)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
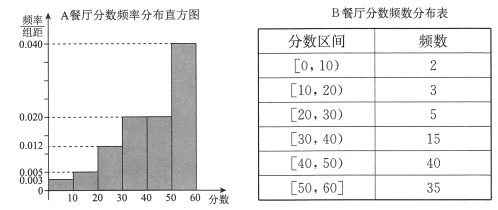
(Ⅰ)在抽样的100人中,求对![]() 餐厅评分低于30的人数;
餐厅评分低于30的人数;
(Ⅱ)从对![]() 餐厅评分在
餐厅评分在![]() 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在![]() 范围内的概率;
范围内的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似地看出两条平行的直线,江岸的一侧有![]() ,
, ![]() 两个蔬菜基地,江岸的另一侧点
两个蔬菜基地,江岸的另一侧点![]() 处有一个超市.已知
处有一个超市.已知![]() 、
、![]() 、
、![]() 中任意两点间的距离为
中任意两点间的距离为![]() 千米,超市欲在
千米,超市欲在![]() 之间建一个运输中转站
之间建一个运输中转站![]() ,
, ![]() ,
, ![]() 两处的蔬菜运抵
两处的蔬菜运抵![]() 处后,再统一经过货轮运抵
处后,再统一经过货轮运抵![]() 处,由于
处,由于![]() ,
, ![]() 两处蔬菜的差异,这两处的运输费用也不同.如果从
两处蔬菜的差异,这两处的运输费用也不同.如果从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元.从
元.从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元,货轮的运输费为每千米
元,货轮的运输费为每千米![]() 元.
元.

(1)设![]() ,试将运输总费用
,试将运输总费用![]() (单位:元)表示为
(单位:元)表示为![]() 的函数
的函数![]() ,并写出自变量的取值范围;
,并写出自变量的取值范围;
(2)问中转站![]() 建在何处时,运输总费用
建在何处时,运输总费用![]() 最小?并求出最小值.
最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的一段图象如下所示.
)的一段图象如下所示. 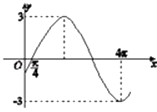
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对边分别为a,b,c且acosC,bcosB,ccosA成等差数列.
(1)求B的值;
(2)求2sin2A﹣1+cos(A﹣C)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com