
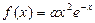 ,
,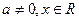 .
.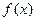 的单调性.
的单调性.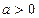 时,讨论关于
时,讨论关于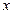 的方程
的方程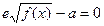 的实根的个数.
的实根的个数.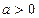 时,
时,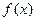 在
在 上单调递增,在
上单调递增,在 和
和 上单调递减. 当
上单调递减. 当 时,
时,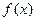 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减(II)即
上单调递减(II)即 时,原方程有一解.
时,原方程有一解. 时,原方程有两解.
时,原方程有两解. 时,原方程有三解.
时,原方程有三解.  , ―――――――――――――――(1分)
, ―――――――――――――――(1分) ,即:
,即: . ―――――――――――――――――――(2分)
. ―――――――――――――――――――(2分)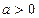 时,
时,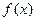 在
在 上单调递增, ―――――――――――――――(4分)
上单调递增, ―――――――――――――――(4分) 和
和 上单调递减. ――――――――――――――――――(6分)
上单调递减. ――――――――――――――――――(6分) 时,
时,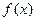 在
在 和
和 上单调递增, ――――――――――――(7分)
上单调递增, ――――――――――――(7分) 上单调递减. ―――――――――――――――――――――――――-(8分)
上单调递减. ―――――――――――――――――――――――――-(8分)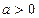 时,
时,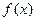 极小=
极小= ,
,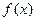 极大=
极大= ――――――――――――――――(9分)
――――――――――――――――(9分) 或
或 时,
时, ,
,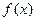 的图象如下: ――――――――――(10分)
的图象如下: ――――――――――(10分)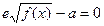 ,
, ――――――――――――(11分)
――――――――――――(11分) 时,即
时,即 时,原方程有一解.
时,原方程有一解. 时,原方程有两解.
时,原方程有两解. 时,原方程有三解. ――――――――-(12分
时,原方程有三解. ――――――――-(12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com