
分析 (1)设这批产品共有x件,根据题意构造方程$\frac{x}{16}$-$\frac{x}{24}$=20,解得答案;
(2)分别讨论出由甲厂单独加工,由乙厂单独加工,由两厂合作加工的费用,比较后,可得答案.
解答 解:(1)设这批产品共有x件,
则$\frac{x}{16}$-$\frac{x}{24}$=20,
解得:x=960,
即这批产品共有960件;
(2)由甲厂单独加工:需要耗时$\frac{960}{16}$=60天,需要费用为:60×(180+10)=11400元;
由乙厂单独加工:需要耗时$\frac{960}{24}$=40天,需要费用为:40×(220+10)=9200元;
由两厂合作加工:需要耗时$\frac{960}{24+16}$=24天,需要费用为:24×(220+10+180+10)=10080元;
故有乙厂单独加工最省钱.
点评 本题考查的知识点是根据实际选择函数模型,一元一次方程的应用,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{{n}^{2}-n+2}{2}$ | B. | an=$\frac{{n}^{2}-n+1}{2}$ | C. | an=$\frac{2}{{n}^{2}-n+1}$ | D. | an=$\frac{2}{{n}^{2}-n+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
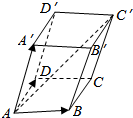 在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.
在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com